Thảo luận:Hình học 10/Chương I/§2. Tổng và hiệu của hai vectơ
giúp mình nha...bài toán:cho tứ giác ABCD.E và F là trung điểm của AB và CD.O là trung điểm của EF.chứng minh vécto DA vécto BC = vécto BC vécto DC
@Hiếu: Cảm ơn cậu, một ví dụ thực tế sinh động cho bài học.
Phép tổng hợp lực theo nguyên tắc hình bình hành của ông Nguyễn Văn Thường có thể tìm thấy tại đây
@Plet: Cảm ơn bạn đã góp ý. Đây là một trang sách về Hình học 10, chủ đề vectơ đối tượng chủ yếu là các giáo viên, học sinh đang dạy và học lớp 10. Vì thế mọi điều trình bày ở đây đều mặc địch được hiểu là đang xét trong Hình học phẳng.
theo mình có góp ý sau. Khi tiếp cận vấn đề thì nên coi nó là gì và nằm trong không gian nào để mà suy xét. Ở đây, là không gian 2 chiều, nó có những phép toán nào được dùng. Và thế ta sẽ suy nghĩ theo lối đó sẽ giải quyết vấn đề.—bàn luận không ký tên trên là của Plet (thảo luận • đóng góp)
Bài này cần viết lại.--
Một ví dụ có nhiều cách giải:
| VÍ DỤ 2 |
Chứng
minh
rằng:
"Với
bốn
điểm
bất
kì
A,
B,
C,
D
ta
luôn
có:
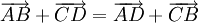 ".
".
Cách 1. Áp dụng quy tắc trừ Thật vậy, lấy điểm một O tùy ý ta có:
Cách 2. Áp dụng quy tắc trừ
Cách 3. Áp dụng quy tắc ba điểm Thật vậy, lấy điểm một O tùy ý ta có:
Cách 4. Áp dụng quy tắc ba điểm Thật vậy, lấy điểm một O tùy ý ta có:
|
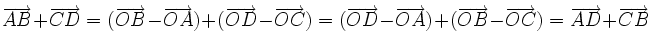
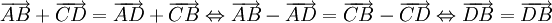

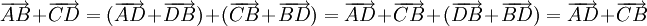



@Giosamac kute: Tôi không hiểu kết luận của bài toán, cần chứng minh gì? Bạn có thể gõ lại không?