Chủ đề nóng: Phương pháp kỷ luật tích cực - Cổ học tinh hoa - Những thói hư tật xấu của người Việt - Công lý: Việc đúng nên làm - Giáo án Điện tử - Sách giáo khoa - Học tiếng Anh - Bài giảng trực tuyến - Món ăn bài thuốc - Chăm sóc bà bầu - Môi trường - Tiết kiệm điện - Nhi khoa - Ung thư - Tác hại của thuốc lá - Các kỹ thuật dạy học tích cực
- Dạy học phát triển năng lực - Chương trình giáo dục phổ thông
Định lý Hurwitz
Từ VLOS
Trong lý thuyết số, Định lý Hurwitz, được đặt tên theo nhà toán học Adolf Hurwitz. Định lý thuộc lĩnh vực xấp xỉ Diophantine (tiếng Anh: Diophantine approximation). Định lý khẳng định rằng với bất kì số vô tỉ ξ luôn tồn tại vô số hữu tỉ m/n sao cho
Giả thiết ξ là số vô tỉ có thể bỏ qua, nghĩa là định lý thỏa mãn cả với ξ là số hữu tỉ (điều này là hiển nhiên).
Hằng
số
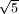 là
tốt
nhất
(là
hằng
số
nhỏ
nhất
đảm
bảo
định
lý
Hurwitz
đúng
với
mọi
số
thực
ξ);
thật
vậy,
nếu
ta
thay
là
tốt
nhất
(là
hằng
số
nhỏ
nhất
đảm
bảo
định
lý
Hurwitz
đúng
với
mọi
số
thực
ξ);
thật
vậy,
nếu
ta
thay
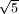 bằng
số
thực
bằng
số
thực
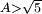 và
chọn
và
chọn
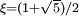 (tỉ
lệ
vàng)
thì
chỉ
tồn
tại
hữu
hạn
số
hữu
tỉ
m/n
thỏa
mãn
công
thức
trên.
(tỉ
lệ
vàng)
thì
chỉ
tồn
tại
hữu
hạn
số
hữu
tỉ
m/n
thỏa
mãn
công
thức
trên.
Chú thích[sửa]
- Hurwitz, A. (1891). "Ueber die angenäherte Darstellung der Irrationalzahlen durch rationale Brüche (On the approximation of irrational numbers by rational numbers)" (in German). Mathematische Annalen 39 (2): 279–284. doi:10.1007/BF01206656. Bản mẫu:JFM.
- G. H. Hardy, Edward M. Wright, Roger Heath-Brown, Joseph Silverman, Andrew Wiles (2008). “Theorem 193”, An introduction to the Theory of Numbers, 6th, Oxford science publications. ISBN 0199219869.
- LeVeque, William Judson (1956), Topics in number theory, Addison-Wesley Publishing Co., Inc., Reading, Mass., Bản mẫu:MathSciNet