GTLN, GTNN trong các kì thi tốt nghiệp THPT
Tìm
giá
trị
nhỏ
nhất
và
giá
trị
lớn
nhất
của
hàm
số
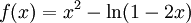 trên
đoạn
[–
2 ;
0].
trên
đoạn
[–
2 ;
0].
Tìm
giá
trị
lớn
nhất
và
giá
trị
nhỏ
nhất
của
hàm
số
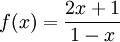 trên
đoạn
[2;
4]
trên
đoạn
[2;
4]
Tìm
giá
trị
lớn
nhất
và
giá
trị
nhỏ
nhất
của
hàm
số
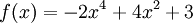 trên
đoạn
[0;
2].
trên
đoạn
[0;
2].
Tìm
giá
trị
lớn
nhất
và
giá
trị
nhỏ
nhất
của
hàm
số
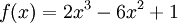 trên
đoạn
[-1;
1].
trên
đoạn
[-1;
1].
Tìm
giá
trị
lớn
nhất
và
giá
trị
nhỏ
nhất
của
hàm
số
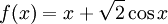 trên
đoạn
trên
đoạn
![\left[0;{\frac {\pi }{2}}\right]](https://tusach.thuvienkhoahoc.com/images/math/f/3/e/f3e7b49af80b8e073a5693f28b7ce6ac.png)
Tìm
giá
trị
lớn
nhất
và
giá
trị
nhỏ
nhất
của
hàm
số
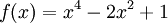 trên
đoạn
[0;
2]
trên
đoạn
[0;
2]
Tìm
giá
trị
lớn
nhất,
giá
trị
nhỏ
nhất
của
hàm
số
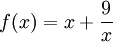 trên
đoạn
[2;
4].
trên
đoạn
[2;
4].
Tìm
giá
trị
lớn
nhất,
giá
trị
nhỏ
nhất
của
hàm
số
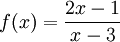 trên
đoạn
[0;
2].
trên
đoạn
[0;
2].
Tìm
giá
trị
lớn
nhất
và
giá
trị
nhỏ
nhất
của
hàm
số
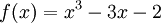 trên
đoạn
[-1;
3].
trên
đoạn
[-1;
3].
Tìm
giá
trị
lớn
nhất
và
giá
trị
nhỏ
nhất
của
hàm
số
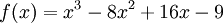 trên
đoạn
[1;
3].
trên
đoạn
[1;
3].
Tìm
giá
trị
lớn
nhất
và
giá
trị
nhỏ
nhất
của
hàm
số
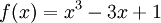 ttrên
đoạn
[0;
2].
ttrên
đoạn
[0;
2].
Tìm
giá
trị
lớn
nhất
của
hàm
số
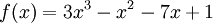 trên
đoạn
[0;
2].
trên
đoạn
[0;
2].
Tìm
giá
trị
lớn
nhất
và
nhỏ
nhất
của
hàm
số
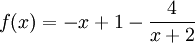 trên
đoạn
[-1;
2].
trên
đoạn
[-1;
2].
Tìm
giá
trị
lớn
nhất
của
hàm
số
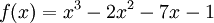 trên
đoạn
[-2;
2].
trên
đoạn
[-2;
2].
Tìm
giá
trị
nhỏ
nhất
của
hàm
số
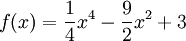 trên
đoạn
[-2;
1].
trên
đoạn
[-2;
1].
Tìm
giá
trị
lớn
nhất
và
giá
trị
nhỏ
nhất
của
hàm
số
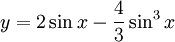 trên
đoạn
[0;
π]
trên
đoạn
[0;
π]
Tìm
giá
trị
lớn
nhất
và
nhỏ
nhất
của
hàm
số
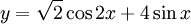 với
với
![x\in \left[0;{\frac {\pi }{2}}\right]](https://tusach.thuvienkhoahoc.com/images/math/3/5/c/35c1792581259c1d4d6963a2ca3b7de6.png)


