Tính lãi vay phải trả

Từ VLOS
(đổi hướng từ Tính Lãi vay phải trả)
Bước tới: chuyển hướng, tìm kiếm

Các khoản vay không phải lúc nào cũng giống nhau. Vì vậy, biết cách tính một khoản nợ phải trả hằng tháng cũng như lãi đến hạn phải trả là rất hữu ích để chọn một khoản vay phù hợp với bạn. Để hiểu chính xác cách tính, bạn có thể phải nghiên cứu công thức tính phức tạp, nhưng cũng có thể tính đơn giản hơn bằng cách dùng Excel.

Các bước[sửa]

Tìm hiểu nhanh về Khoản vay[sửa]

  1. Nhập thông tin về khoản vay vào chương trình tính toán trên mạng sẽ giúp bạn nhanh chóng tính được lãi phải trả. Tuy nhiên, phương trình tính lãi lại không hề đơn giản. Thật may là chỉ bằng cách tra trên mạng cụm từ "chương trình tính lãi phải trả" (interest payment calculator), bạn dễ dàng tìm ra được kết quả sau khi điền các thông số vào máy tính như sau:
    • Nợ gốc: Giá trị khoản vay. Nếu khoản vay là 5.000 USD, nợ gốc sẽ là 5.000 USD.
    • Lãi suất: Đơn giản là tỷ lệ phần trăm số tiền bạn phải trả để được vay. Có thể quy định lãi suất dưới dạng tỷ lệ phần trăm (chẳng hạn như 4%) hoặc số thập phân (0,04).
    • Kỳ hạn: Thường được tính theo tháng, đó là thời hạn bạn phải trả nợ. Đối với các khoản thế chấp, kỳ hạn tính theo năm.
    • Hình thức thanh toán: Phần lớn là "vay kỳ hạn cố định." Tuy nhiên, phương thức này có thể khác đối với các khoản vay đặc biệt. Nếu bạn không chắc hãy hỏi liệu lãi và thời hạn thanh toán có cố định không trước khi đi vay.[1]
  2. Tìm hiểu về lãi suất trước khi vay. Lãi suất là phí phải trả để được vay. Đó là mức lãi bạn phải trả trên khoản vay gốc suốt kỳ hạn đi vay. Tỷ lệ này càng thấp càng tốt, thậm chí chỉ cần khác 0,5% cũng là cả một khoản tiền lớn.[2] Nếu bạn chọn nợ phải trả định kỳ thấp hơn, bạn có thể phải trả lãi suất cao hơn và tổng tiền lãi nhiều hơn nhưng khoản thanh toán mỗi tháng sẽ ít đi. Những người có ít tiền tiết kiệm hay thu nhập dựa vào tiền hoa hồng và tiền thưởng thường thích lựa chọn này. Tuy vậy, cố gắng chỉ vay với lãi suất dưới 10% bất cứ lúc nào có thể. Các mức lãi suất thông thường đối với một số khoản vay như sau:
    • Vay mua ô tô: 4-7% [3]
    • Vay mua nhà: 3-6%
    • Vay cá nhân: 5-9%
    • Thẻ tín dụng: 18-22%. Đó là lý do tại sao bạn tránh mua cái gì nhiều tiền mà không thể trả ngay nợ thẻ tín dụng.
    • Vay theo ngày (vay nóng): 350-500%. Vay kiểu này rất nguy hiểm nếu bạn không thể thanh toán trong vòng 1-2 tuần.[4]
  3. Hãy hỏi tỷ suất tích lũy để biết khi nào bạn phải trả lãi. Tỷ suất tích lũy cho bạn biết tần suất chủ nợ tính lãi bạn phải trả. Tần suất trả nợ càng cao thì nợ càng nhiều vì bạn có ít thời gian trả nợ nhưng đổi lại bạn không phải trả lãi cao.[5] Ví dụ, hãy xem khoản vay 100.000 USD, lãi suất kép 4% được tính theo ba cách cho kết quả như thế nào:
    • Theo năm: 110.412,17 USD
    • Theo tháng: 110.512,24 USD
    • Theo ngày: 110.521,28 USD
  4. Vay dài hạn thì tiền trả mỗi tháng ít hơn nhưng tổng lãi sẽ cao hơn. Kỳ hạn là khoảng thời gian bạn phải hoàn trả nợ.[6] Mỗi khoản vay có kỳ hạn khác nhau và bạn cần phải chọn khoản vay có kỳ hạn phù hợp với nhu cầu. Kỳ hạn dài thường cho kết quả là tổng lãi cao hơn nhưng tiền phải trả hằng tháng thấp hơn.[4] Giả sử bạn vay 20.000 USD để mua ô tô với lãi suất 5%. Tổng khoản nợ phải trả sẽ là:
    • Kỳ hạn 24 tháng: Bạn phải trả tổng lãi là 1.058,27 USD, nhưng mỗi tháng chỉ phải trả cả gốc lẫn lãi là 877,43 USD.
    • Kỳ hạn 30 tháng: Bạn phải trả tổng lãi là 1.317,63 USD, nhưng chỉ phải trả cả gốc lẫn lãi là 710,59 USD hằng tháng.
    • Kỳ hạn 36 tháng: Bạn phải trả tổng lãi là 1.579,02 USD, trong khi gốc và lãi phải trả mỗi tháng chỉ là 599,42 USD.[1]

Tính nhẩm Khoản thanh toán[sửa]

  1. Học công thức tính lãi kép. Tính các khoản nợ phải trả định kỳ và lãi dùng công thức toán học sau: 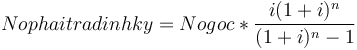Nophaitradinhky=Nogoc*{\frac {i(1+i)^{n}}{(1+i)^{n}-1}} [7]
    • "i" là lãi suất, "n" là số lần thanh toán.
    • Giống như hầu hết các phương trình tài chính, công thức tính khoản nợ phải trả định kỳ phức tạp hơn nhiều so với tính toán đơn thuần. Khi hiểu được nguyên lý của các con số thì bạn sẽ thấy tính toán khoản nợ phải trả định kỳ vô cùng dễ.
  2. Điều chỉnh tần suất trả nợ. Trước khi lắp số vào phương trình, bạn phải điều chỉnh kỳ hạn trả lãi suất “i”.
    • Chẳng hạn, giả sử bạn đi vay với lãi suất 4,5%/năm, trả nợ hằng tháng.
    • Vì phải trả nợ hằng tháng nên bạn chia lãi suất cho 12. 4,5% (0,045) chia cho 12 bằng 0,00375. Lắp kết quả vào "i".[7]
  3. Điều chỉnh số lần trả nợ. Để xác định "n" là bao nhiêu, bước tiếp theo là xác định tổng số lần trả nợ trong suốt kỳ hạn đi vay.
    • Giả sử bạn phải trả nợ hằng tháng cho khoản vay kéo dài 30 năm. Để tìm số lần phải trả nợ, hãy nhân 30 với 12. Bạn sẽ tính được số lần trả nợ là 360.[7]
  4. Tính khoản nợ phải trả hằng tháng. Để tìm giá trị khoản nợ trả hằng tháng của khoản vay, bạn hãy lắp các con số vào công thức. Trông có vẻ đáng sợ, nhưng bạn cứ làm từ từ rồi sẽ sớm có kết quả thôi. Dưới đây là các bước tính toán, hãy làm lần lượt từng bước.
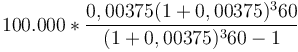
    • Tiếp tục với ví dụ trên, giả sử bạn vay 100.000 USD. Phương trình sẽ như sau: 100.000*{\frac {0,00375(1+0,00375)^{3}60}{(1+0,00375)^{3}60-1}}

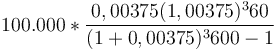
    • 100.000*{\frac {0,00375(1,00375)^{3}60}{(1+0,00375)^{3}600-1}}

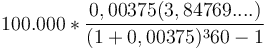
    • 100.000*{\frac {0,00375(3,84769....)}{(1+0,00375)^{3}60-1}}

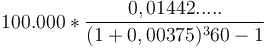
    • 100.000*{\frac {0,01442.....}{(1+0,00375)^{3}60-1}}

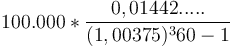
    • 100.000*{\frac {0,01442.....}{(1,00375)^{3}60-1}}

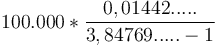
    • 100.000*{\frac {0,01442.....}{3,84769.....-1}}

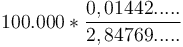
    • 100.000*{\frac {0,01442.....}{2,84769.....}}

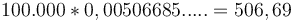
    • 100.000*0,00506685.....=506,69

    • 506,69 USD. Đây là khoản nợ bạn phải trả hằng tháng.
  5. Tính tổng lãi phải trả. Bạn đã có kết quả khoản nợ phải trả hằng tháng, giờ bạn có thể tính được tổng lãi phải trả trong kỳ hạn vay. Nhân số lần thanh toán trong suốt kỳ hạn đi vay với giá trị khoản nợ phải trả hằng tháng. Sau đó trừ nợ gốc.[7]
    • Sử dụng ví dụ ở trên, nhân 360 với 506,69 USD ta được 182.408 USD. Đây là tổng số tiền bạn phải trả trong suốt kỳ hạn đi vay.
    • Trừ 100.000 USD và kết quả là 82.408 USD. Đó là tổng lãi bạn phải trả khi hết thời hạn vay.

Tính Lãi bằng Excel[sửa]

  1. Ghi nợ gốc, kỳ hạn và lãi suất đi vay vào một cột. Các ô khác bạn ghi giá trị của chúng và Excel sẽ tính nợ phải trả hằng tháng giúp bạn. Trong phần còn lại của bài viết này, bạn có thể sử dụng ví dụ sau:
    • Bạn vay 100.000 USD để mua nhà với lãi suất 4,5%/năm, thời hạn 30 năm.
  2. Ghi nợ gốc là số âm. Bạn cần cho Excel biết bạn đang trả nợ. Do đó, bạn phải ghi là số âm, không có ký hiệu tiền tệ ($).
    • -100.000 = Nợ gốc
  3. Xác định số lần trả nợ. Bạn có thể để là năm nếu muốn nhưng kết quả sẽ là nợ trả theo năm không phải là tháng. Vì hầu hết các khoản vay đều trả theo tháng, bạn chỉ cần nhân số năm với 12 để có tổng số lần trả nợ. Ghi kết quả này vào một ô khác.
    • -100.000 = Nợ gốc
    • 360 = Số lần trả nợ
  4. Đổi lãi suất để phù hợp với số lần trả nợ. Trong trường hợp này, lãi suất tính theo năm, nghĩa là lãi sẽ được tính vào cuối năm. Tuy nhiên, bạn phải trả nợ hằng tháng, nghĩa là bạn cần biết lãi suất trả hằng tháng là bao nhiêu. Vì 4,5% là lãi suất 12 tháng, hãy chia cho 12 để được lãi suất mỗi tháng. Nhớ chuyển tỷ lệ phần trăm sang số thập phân sau khi có kết quả.
    • -100.000 = Nợ gốc
    • 360 = Số lần trả nợ
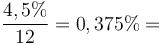
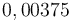    • {\frac {4,5\%}{12}}=0,375\%=0,00375 = Lãi phải trả hằng tháng.
  5. Dùng hàm =PMT để tính lãi phải trả. Excel biết cách tính các khoản trả nợ hằng tháng nếu biết lãi là bao nhiêu. Vì vậy, bạn chỉ cần điền thông tin để Excel tính. Nhấp chuột vào một ô trống, rồi tìm thanh hàm số. Thanh công cụ nằm bên phải ngay trên bảng tính (spreadsheet), ký hiệu là "fx". Nhấp vào đó và ghi "=PMT("
    • Không điền dấu ngoặc kép.
    • Nếu giỏi Excel, bạn có thể tạo công thức Excel để tính giá trị nợ phải trả.
  6. Điền dữ liệu vào đúng vị trí. Cho các giá trị để tính nợ phải trả vào ngoặc đơn, cách nhau bằng dấu phẩy. Trong trường hợp này, bạn phải điền (lãi suất, kỳ hạn, nợ gốc,0).
    • Với ví dụ nêu trên, dữ liệu đầy đủ là: "=PMT(0,00375,360,-100000,0)"
    • Số cuối cùng trong dãy số là 0. Số 0 nghĩa là dư nợ cuối kỳ (360 lần trả nợ) sẽ bằng 0 USD.
    • Nhớ đóng ngoặc lại.
  7. Nhấn phím Enter để được kết quả nợ trả hằng tháng. Nếu bạn điền công thức đúng, bạn sẽ thấy kết quả trong ô công thức =PMT trên bảng tính.
    • Trong trường hợp này, kết quả sẽ là 506,69 USD. Đó chính là nợ phải trả hằng tháng của bạn.
    • Nếu bạn nhìn thấy lỗi "#NUM!" hoặc một kết quả khác không có ý nghĩa, chứng tỏ bạn đã nhập dữ liệu chưa đúng. Hãy kiểm tra lại công thức trên thanh hàm số và thử lại.
  8. Tính tổng nợ phải trả bằng cách nhân với số lần trả nợ. Để tính tổng số tiền bạn phải trả suốt thời gian đi vay, bạn chỉ cần nhân nợ phải trả định kỳ với số lần trả nợ.
    • Trong ví dụ trên, bạn nhân 506,69 USD với 360 để được kết quả 182.408 USD. Đây là tổng số tiền phải trả cuối kỳ vay.
  9. Tính lãi bằng cách lấy tổng số tiền phải trả trừ nợ gốc. Nếu muốn biết tổng lãi phải trả, bạn chỉ cần làm phép tính trừ. Hãy lấy tổng nợ phải trả cuối kỳ trừ nợ gốc.
    • Trong ví dụ này, bạn lấy 182.408 USD trừ cho 100.000 USD. Kết quả thu được là 82.408 USD. Đó là tổng lãi vay phải trả.

Làm Bảng tính mẫu để Tính Lãi vay[sửa]

Bảng dưới đây sẽ chỉ ra cách tính lãi vay sử dụng Excel, Google Docs, hoặc các chương trình bảng tính tương tự. Chỉ cần điền số vào. Chú ý là khi thấy công thức 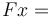Fx= , bạn phải điền dữ liệu vào công thức trên thanh hàm số "Fx". Các số (A2, C1, v.v...) tương ứng với các ô được gán nhãn trong Excel và Google Docs.

Bảng tính Lãi vay mẫu
 A    B    C    D  
1 [Nợ gốc] [Số lần trả nợ] [Lãi suất] [Lãi suất/tháng]
2 Khoản vay âm (-100000) Tổng số lần trả nợ theo tháng. (360) Lãi suất, ghi bằng số thập phân. (0,05) Lãi suất/tháng (chia lãi suất/năm cho 12)
3 Nợ trả/tháng FX=PMT(D2,B2,A2,0). CHÚ Ý: Số cuối cùng là số 0.
4 Tổng tiền vay FX=PRODUCT(D3,B2)
5 Lãi vay FX=SUM(D4,A2)

Lời khuyên[sửa]

  • Hiểu được cách tính khoản vay sẽ cho bạn công cụ để loại bớt những khoản vay không phù hợp.
  • Nếu bạn có những nguồn thu nhập không liên tục và đang xem xét một khoản vay có lãi suất không thật thấp nhưng nợ phải trả định kỳ thấp với tần suất trả ít hơn thì nên chọn khoản vay có thời hạn vay dài hơn, dù tổng lãi vay lớn hơn.
  • Nếu bạn tiết kiệm được nhiều hơn cần thiết và muốn tìm những khoản vay có lãi suất thấp nhất để đáp ứng nhu cầu của mình thì khoản vay có thời hạn ngắn, nợ phải trả định kỳ cao và ít lãi hơn sẽ phù hợp với bạn.

Cảnh báo[sửa]

  • Có nhiều lúc lãi suất thấp nhất không có nghĩa là chi phí đi vay ít nhất. Nếu hiểu cặn kẽ được cách tính lãi thì bạn có thể nhanh chóng tính được “chi phí” thực sự của khoản vay so với cái giá phải trả để được một số mặt lợi của khoản vay đó.

Nguồn và Trích dẫn[sửa]

  1. ↑ 1,0 1,1 http://www.interest.com/home-equity/calculators/monthly-payment-calculator/
  2. ↑ http://www.investopedia.com/terms/i/interestrate.asp
  3. ↑ http://www.bankrate.com/finance/auto/current-interest-rates.aspx
  4. ↑ 4,0 4,1 http://econlib.org/library/Enc/InterestRates.html
  5. ↑ http://www.investopedia.com/terms/a/accrual-rate.asp
  6. ↑ http://www.investopedia.com/terms/t/term.asp
  7. ↑ 7,0 7,1 7,2 7,3 http://www.fonerbooks.com/interest.htm
  • « Mới nhất
  • ‹ Mới hơn
  • Cũ hơn ›

Liên kết đến đây

Lấy từ “https://tusach.thuvienkhoahoc.com/index.php?title=Tính_lãi_vay_phải_trả&oldid=143415”