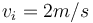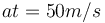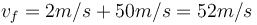Chủ đề nóng: Phương pháp kỷ luật tích cực - Cổ học tinh hoa - Những thói hư tật xấu của người Việt - Công lý: Việc đúng nên làm - Giáo án Điện tử - Sách giáo khoa - Học tiếng Anh - Bài giảng trực tuyến - Món ăn bài thuốc - Chăm sóc bà bầu - Môi trường - Tiết kiệm điện - Nhi khoa - Ung thư - Tác hại của thuốc lá - Các kỹ thuật dạy học tích cực
- Dạy học phát triển năng lực - Chương trình giáo dục phổ thông
Tính vận tốc
Từ VLOS
(đổi hướng từ Tính Vận tốc)
Tốc độ là độ nhanh khi di chuyển theo một chiều nhất định của vật thể. Về mặt toán học, tốc độ thường được xem là sự thay đổi vị trí của một vật theo thời gian. Khái niệm cơ bản này có mặt trong rất nhiều bài toán vật lý. Nên sử dụng công thức nào phụ thuộc vào những gì đã biết của vật thể, để chọn được công thức đúng, hãy đọc kỹ bài viết này.
Mục lục
Công thức Rút gọn[sửa]
-
Vận
tốc
trung
bình
=
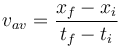
-
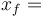 vị
trí
cuối
cùng
vị
trí
cuối
cùng
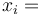 vị
trí
ban
đầu
vị
trí
ban
đầu -
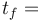 thời
điểm
cuối
thời
điểm
cuối
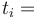 thời
điểm
ban
đầu
thời
điểm
ban
đầu
-
-
Vận
tốc
trung
bình
khi
gia
tốc
là
hằng
số
=
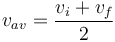
-
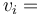 vận
tốc
ban
đầu
vận
tốc
ban
đầu
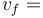 vận
tốc
cuối
vận
tốc
cuối
-
-
Vận
tốc
trung
bình
nếu
gia
tốc
là
hằng
số
bằng
0
=
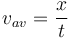
-
Vận
tốc
cuối
=
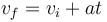
- a = gia tốc t = thời gian
Các bước[sửa]
Tìm Vận tốc Trung bình[sửa]
-
Tìm
vận
tốc
trung
bình
khi
gia
tốc
là
hằng
số.
Nếu
một
vật
thể
có
gia
tốc
không
đổi,
công
thức
tính
vận
tốc
trung
bình
rất
đơn
giản:
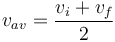 .
Trong
đó,
.
Trong
đó,
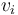 là
vận
tốc
ban
đầu,
và
là
vận
tốc
ban
đầu,
và
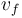 là
vận
tốc
cuối
cùng.
Chỉ
dùng
công
thức
này
nếu
gia
tốc
là
hằng
số.
là
vận
tốc
cuối
cùng.
Chỉ
dùng
công
thức
này
nếu
gia
tốc
là
hằng
số.
-
Ví
dụ:
xét
một
đoàn
tàu
có
gia
tốc
không
đổi
từ
30
m/s
đến
80
m/s.
Vậy
vận
tốc
trung
bình
của
đoàn
tàu
là
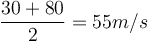 .
.
-
Ví
dụ:
xét
một
đoàn
tàu
có
gia
tốc
không
đổi
từ
30
m/s
đến
80
m/s.
Vậy
vận
tốc
trung
bình
của
đoàn
tàu
là
-
Xây
dựng
công
thức
sử
dụng
vị
trí
và
thời
gian.
Bạn
có
thể
tính
được
vận
tốc
dựa
vào
sự
thay
đổi
vị
trí
theo
thời
gian
của
vật
thể
đó.
Cách
này
có
thể
áp
dụng
ở
mọi
trường
hợp.
Chú
ý
rằng,
trừ
khi
vật
thể
di
chuyển
với
tốc
độ
không
đổi,
kết
quả
bạn
tính
được
sẽ
là
vận
tốc
trung
bình
trong
khi
di
chuyển
chứ
không
phải
là
vận
tốc
tức
thời
tại
một
thời
điểm
nào
đó.
-
Công
thức
trong
trường
hợp
này
là
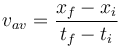 ,
tức
là
"vị
trí
cuối
–
vị
trí
ban
đầu
chia
cho
thời
gian
cuối
–
thời
gian
ban
đầu".
Bạn
cũng
có
thể
viết
lại
công
thức
này
thành
,
tức
là
"vị
trí
cuối
–
vị
trí
ban
đầu
chia
cho
thời
gian
cuối
–
thời
gian
ban
đầu".
Bạn
cũng
có
thể
viết
lại
công
thức
này
thành
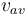 =
Δx
/
Δt,
hoặc
"sự
thay
đổi
vị
trí
theo
thời
gian".
=
Δx
/
Δt,
hoặc
"sự
thay
đổi
vị
trí
theo
thời
gian".
-
Công
thức
trong
trường
hợp
này
là
-
Tìm
khoảng
cách
giữa
điểm
đầu
và
điểm
cuối.
Khi
đo
vận
tốc,
có
hai
điểm
duy
nhất
cần
lưu
ý
là
điểm
khởi
đầu
và
điểm
kết
thúc
của
chuyển
động.
Cùng
với
hướng
chuyển
động,
điểm
đầu
và
điểm
cuối
sẽ
giúp
ta
xác
định
được
sự
dịch
chuyển
hay
nói
cách
khác
là
sự
thay
đổi
vị
trí
của
vật
đang
xét.[1]
Không
cần
xét
đến
quãng
đường
nằm
giữa
hai
điểm
này.
-
Ví
dụ
1:
Một
chiếc
xe
hơi
chạy
về
hướng
đông
xuất
phát
ở
vị
trí
x
=
5
mét.
Sau
8
giây,
chiếc
xe
ở
vị
trí
x
=
41
mét.
Hỏi
chiếc
xe
đã
dịch
chuyển
được
bao
xa?
- Chiếc xe đã dịch chuyển được (41m-5m) = 36 mét về phía đông.
-
Ví
dụ
2:
Một
vận
động
viên
lặn
bật
cao
1
mét
so
với
ván
dậm
nhảy,
sau
đó
rơi
5
mét
trước
khi
tiếp
nước.
Hỏi
vận
động
viên
đó
đã
dịch
chuyển
bao
nhiêu?
- Tổng cộng vận động viên lặn đã di chuyển 4 mét về phía dưới so với vị trí ban đầu, tức là đã dịch chuyển xuống dưới 4 mét, hay nói cách khác là -4 mét. (0 + 1 - 5 = -4). Mặc dù tổng quãng đường di chuyển là 6 mét (1 mét lên trên khi nhảy và 5 mét khi rơi xuống), vấn đề nằm ở chỗ điểm cuối của chuyển động là dưới vị trí ban đầu 4 mét.
-
Ví
dụ
1:
Một
chiếc
xe
hơi
chạy
về
hướng
đông
xuất
phát
ở
vị
trí
x
=
5
mét.
Sau
8
giây,
chiếc
xe
ở
vị
trí
x
=
41
mét.
Hỏi
chiếc
xe
đã
dịch
chuyển
được
bao
xa?
-
Tính
thay
đổi
về
thời
gian.
Vật
thể
đang
xét
mất
bao
lâu
để
đến
được
điểm
cuối?
Có
nhiều
bài
tập
sẽ
cho
sẵn
dữ
kiện
này.
Nếu
không
cho
sẵn,
bạn
có
thể
xác
định
bằng
cách
lấy
thời
điểm
cuối
trừ
thời
điểm
đầu.
- Ví dụ 1 (tiếp): Đề bài cho biết rằng chiếc xe hơi mất 8 giây để đi từ điểm đầu cho tới điểm cuối, vì thế đây là mức thay đổi về thời gian.
- Ví dụ 2 (tiếp): Nếu vận động viên dậm nhảy ở thời điểm t = 7 giây và tiếp nước khi t = 8 giây, sự thay đổi về thời gian = 8 giây – 7 giây = 1 giây.
-
Chia
quãng
đường
cho
thời
gian
dịch
chuyển.
Để
xác
định
vận
tốc
của
một
vật
thể
di
chuyển,
ta
lấy
quãng
đường
đã
di
chuyển
được
chia
cho
tổng
thời
gian
tiêu
tốn
kèm
theo
xác
định
hướng
của
chuyển
động,
bạn
sẽ
được
vận
tốc
trung
bình
của
vật
thể
đó.
-
Ví
dụ
1
(tiếp):
Chiếc
xe
hơi
đã
di
chuyển
được
quãng
đường
là
36
mét
trong
8
giây.
Ta
có
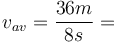 4.5
m/s
về
phía
đông.
4.5
m/s
về
phía
đông. -
Ví
dụ
2
(tiếp):
Vận
động
viên
đã
di
chuyển
quãng
đường
là
-4
mét
trong
1
giây.
Ta
có
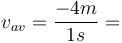 -4
m/s.
(Trong
chuyển
động
một
chiều,
số
âm
thường
mang
hàm
ý
là
"xuống
dưới"
hoặc
"về
bên
trái".
Trong
ví
dụ
này,
ta
có
thể
cho
đáp
án
là
"4
m/s
theo
hướng
xuống
dưới").
-4
m/s.
(Trong
chuyển
động
một
chiều,
số
âm
thường
mang
hàm
ý
là
"xuống
dưới"
hoặc
"về
bên
trái".
Trong
ví
dụ
này,
ta
có
thể
cho
đáp
án
là
"4
m/s
theo
hướng
xuống
dưới").
-
Ví
dụ
1
(tiếp):
Chiếc
xe
hơi
đã
di
chuyển
được
quãng
đường
là
36
mét
trong
8
giây.
Ta
có
-
Trong
trường
hợp
chuyển
động
hai
chiều.
Không
phải
tất
cả
các
bài
tập
đều
bao
gồm
chuyển
động
theo
một
đường
cố
định
nào
đó.
Nếu
vật
thể
thay
đổi
hướng
vào
thời
điểm
nào
đó,
bạn
cần
vẽ
đồ
thị
và
giải
bài
toán
hình
học
để
tìm
được
khoảng
cách.
-
Ví
dụ
3:
Một
người
đi
bộ
3
mét
về
phía
đông,
sau
đó
quay
90
độ
và
đi
thêm
4
mét
về
phía
bắc.
Hỏi
người
này
đã
dịch
chuyển
được
bao
nhiêu?
- Vẽ một đồ thị và nối điềm đầu với điểm cuối thành một đường thẳng. Ta được một tam giác vuông, sử dụng tính chất của tam giác vuông ta sẽ tính được độ dài cạnh của nó. Ở ví dụ này, quãng đường dịch chuyển được là 5 mét về phía đông bắc.
- Đôi khi giáo viên có thể yêu cầu bạn tìm chính xác hướng di chuyển (góc phía trên phương nằm ngang). Bạn có thể sử dụng các tính chất hình học hoặc vẽ véc-tơ để giải quyết vấn đề đó.[2]
-
Ví
dụ
3:
Một
người
đi
bộ
3
mét
về
phía
đông,
sau
đó
quay
90
độ
và
đi
thêm
4
mét
về
phía
bắc.
Hỏi
người
này
đã
dịch
chuyển
được
bao
nhiêu?
Tìm Vận tốc khi biết Gia tốc[sửa]
-
Công
thức
tính
vận
tốc
của
một
vật
có
gia
tốc.
Gia
tốc
là
sự
thay
đổi
vận
tốc.
Vận
tốc
biến
đổi
đều
khi
gia
tốc
là
hằng
số.
Ta
có
thể
mô
tả
sự
thay
đổi
này
bằng
cách
lấy
gia
tốc
nhân
với
thời
gian
sau
đó
cộng
với
vận
tốc
ban
đầu:
-
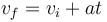 ,
or
"vận
tốc
cuối
=
vận
tốc
ban
đầu
+
(gia
tốc*
thời
gian)"
,
or
"vận
tốc
cuối
=
vận
tốc
ban
đầu
+
(gia
tốc*
thời
gian)" -
Vận
tốc
ban
đầu
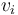 đôi
khi
được
viết
là
đôi
khi
được
viết
là
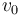 ("vận
tốc
tại
thời
điểm
t
=
0").
("vận
tốc
tại
thời
điểm
t
=
0").
-
-
Tính
tích
gia
tốc
và
thời
gian.
Tích
số
của
gia
tốc
và
thời
gian
cho
biết
vận
tốc
đã
tăng
(hoặc
giảm)
thế
nào
trong
khoảng
thời
gian
đó.
-
Ví
dụ:
Một
con
tàu
chạy
về
hướng
bắc
với
vận
tốc
là
2
m/s
và
gia
tốc
10
m/s2.
Hỏi
vận
tốc
của
tàu
tăng
lên
bao
nhiêu
trong
5
giây
tiếp
theo?
- a = 10 m/s2
- t = 5 giây
- Vận tốc đã tăng (a * t) = (10 m/s2 * 5 s) = 50 m/s.
-
Ví
dụ:
Một
con
tàu
chạy
về
hướng
bắc
với
vận
tốc
là
2
m/s
và
gia
tốc
10
m/s2.
Hỏi
vận
tốc
của
tàu
tăng
lên
bao
nhiêu
trong
5
giây
tiếp
theo?
-
Cộng
với
vận
tốc
ban
đầu.
Khi
đã
biết
sự
thay
đổi
về
vận
tốc,
ta
lấy
giá
trị
này
cộng
với
vận
tốc
ban
đầu
của
vật
để
được
vận
tốc
cần
tìm.
-
Ví
dụ
(tiếp):
Ở
ví
dụ
này,
sau
5
giây
con
tàu
có
vận
tốc
là
bao
nhiêu?
-
-
Ví
dụ
(tiếp):
Ở
ví
dụ
này,
sau
5
giây
con
tàu
có
vận
tốc
là
bao
nhiêu?
-
Xác
định
hướng
của
chuyển
động.
Không
giống
như
tốc
độ,
vận
tốc
luôn
đi
kèm
với
hướng
chuyển
động.
Vì
thế
bạn
hãy
nhớ
luôn
ghi
hướng
của
chuyển
động
khi
nhắc
đến
vận
tốc.
- Trong ví dụ ở trên, vì con tàu luôn chuyển động về hướng bắc và không đổi hướng trong suốt thời gian đó, do vậy vận tốc của nó là 52 m/s về phía bắc.
- Giải các bài tập liên quan. Khi bạn biết gia tốc và vận tốc của vật tại một thời điểm nào đó, bạn có thể sử dụng công thức này để tính vận tốc ở một thời điểm bất kỳ.
Vận tốc Chuyển động Tròn[sửa]
-
Công
thức
tính
vận
tốc
của
chuyển
động
tròn.
Vận
tốc
của
chuyển
động
tròn
là
vận
tốc
một
vật
thể
cần
đạt
được
để
duy
trì
quỹ
đạo
tròn
xung
quanh
một
vật
thể
khác
như
một
hành
tinh
hay
một
vật
thể
có
trọng
lượng.[3]
- Vận tốc chuyển động tròn của một vật được tính bằng cách lấy chu vi của quỹ đạo chia cho thời gian chuyển động.
-
Công
thức
tính
như
sau:
- v = (2πr) / T
- Chú ý: 2πr là chu vi của quỹ đạo của chuyển động
- r là "bán kính"
- T là "khoảng thời gian chuyển động"
-
Nhân
bán
kính
của
quỹ
đạo
chuyển
động
với
2π.
Bước
đầu
tiên
là
tính
chu
vi
của
quỹ
đạo
bằng
cách
lấy
tích
số
của
bán
kính
và
2π.
Nếu
không
dùng
công
cụ
tính
toán,
bạn
có
thể
lấy
π
=
3,14.
-
Ví
dụ :
tính
vận
tốc
chuyển
động
tròn
của
một
vật
có
bán
kính
của
quỹ
đạo
di
chuyển
là
8
mét
trong
thời
gian
45
giây.
- r = 8 m
- T = 45 giây
- Chu vi = 2πr = ~ (2)(3,14)(8 m) = 50,24 m
-
Ví
dụ :
tính
vận
tốc
chuyển
động
tròn
của
một
vật
có
bán
kính
của
quỹ
đạo
di
chuyển
là
8
mét
trong
thời
gian
45
giây.
-
Lấy
chu
vi
chia
cho
thời
gian
chuyển
động.
Để
tính
được
vận
tốc
chuyển
động
tròn
của
vật
thể
trong
đề
bài,
ta
lấy
chu
vi
vừa
tính
được
chia
cho
thời
gian
chuyển
động
của
vật.
-
Ví
dụ:
v
=
(2πr)
/
T
=
50,24
m
/
45
s
=
1,12
m/s
- Vận tốc chuyển động tròn của vật là 1,12 m/s.
-
Ví
dụ:
v
=
(2πr)
/
T
=
50,24
m
/
45
s
=
1,12
m/s
Lời khuyên[sửa]
- Mét trên giây (m/s) là đơn vị vận tốc chuẩn. Cần kiểm tra lại để chắc rằng quãng đường được tính theo mét và thời gian được tính theo giây, đối với gia tốc thì đơn vị chuẩn là mét trên giây trên giây (m/s2).