Thành viên:Phạm Thạch Thảo/Note: Nhiệt động học hình thức

Nhiệt động lực học hay nhiệt động học là phân môn vật lý nghiên cứu sự vận động của năng lượng giữa các dạng khác nhau xoay quanh khái niệm nhiệt lượng.

Nhiệt động học bắt đầu từ việc khảo sát hình thức các quá trình chuyển hóa nhiệt và công, các động cơ nhiệt. Cuối thế kỷ 19, các nhà vật lý đã xây dựng thành công các nguyên lý mô tả hình thức các quá trình chuyển hóa năng lượng đó. Ngày nay các nguyên lý này được biết đến như những nguyên lý của nhiệt động học các quá trình cân bằng.

Với sự phát triển của vật lý thống kê, nhiệt động học các quá trình cân bằng thường được coi như một phần rút ra từ hệ thống lý thuyết của các quá trình vi mô. Tuy nhiên, các nguyên lý của nhiệt động học mang tính độc lập tương đối, và trong thế kỷ 20 cũng có nhiều nỗ lực hoàn thiện hệ thống lý thuyết của nhiệt động học như một phần độc lập. Nhiều cố gắng tập trung vào việc hình thức hóa nhiệt động học dựa trên cơ sở toán trừu tượng [trích: Foundation of Thermodynamics]. Tuy nhiên thành công đặc biệt phải kể đến sự kiện giữa thế kỷ 20, khi lý thuyết thông tin phát triển hết sức mạnh mẽ đã giúp một phần rất đáng kể vào việc soi sáng các nguyên lý của Nhiệt động học [trích dẫn Jaynes].

Cùng với vật lý thống kê, nhiệt động học phát triển đến khảo sát các quá trình không cân bằng, được gọi là nhiệt động học các quá trình không cân bằng. Trong bài này, chúng ta dùng nhiệt động học với nghĩa là lý thuyết cho các quá trình cân bằng.

Một số khái niệm

Các hệ vật lý tham gia trong các quá trình chuyển hóa năng lượng liên quan đến nhiệt lượng (tức là đối tượng của nhiệt động lực học) được gọi là các hệ nhiệt động. [cmt: Cần phân biệt hệ nhiệt động cân bằng và không cân bằng, cũng có thể tiến hành phân loại ở dưới.]

Thông số (tham số) nhiệt động là các đại lượng vĩ mô đo được, đặc trưng cho hệ đang xét như áp suất, thể tích .... Những đại lượng này được rút ra từ thực nghiệm.[cmt: không nhất thiết, entropy không rút ra từ thực nghiệm] Có hai loại thông số nhiệt động:

• Thông số ngoại: là những đại lượng xác định bởi vị trí các vật bên ngoài, không tham gia vào hệ đang xét.

Ví dụ: Thể tích là một thông số ngoại do nó được xác định bởi vị trí các vật bên ngoài hệ.

• Thông số nội: là các đại lượng được xác định bởi tập hợp phân bố và chuyển động của các hạt xác lập nên hệ.

Ví dụ: Áp suất, năng lượng của hệ ...

Trạng thái của hệ nhiệt động được xác định bởi tập hợp các thông số nhiệt động của hệ, cần thiết để mô tả hệ đó.

Trạng thái cân bằng nhiệt động là trạng thái khi đó các tham số nhiệt động của hệ không đổi theo thời gian và không có những dòng dừng do tác động của các nguồn bên ngoài gây ra trong hệ.

Hệ cô lập là hệ không trao đổi năng lượng với các vật bên ngoài.

Phương trình trạng thái là hàm mô tả quan hệ giữa các tham số nhiệt động của hệ ở trạng thái cân bằng, thường có dạng:

$f(P,V,T)=0$

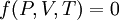
Các luận điểm xuất phát và nguyên lý

Luận điểm thứ nhất của nhiệt động học nói rằng "với thời gian, hệ cô lập bao giờ cũng chuyển sang trạng thái cân bằng nhiệt động và không bao giờ có thể tự nó thoát ra khỏi trạng thái ấy" (đang thảo luận [cmt: đây thực sự là các trình bày của Bazarov, ta xem thêm phần hình thức hóa nhiệt động học cuối bài, và Callen để tham khảo];)

Luận điểm thứ hai của nhiệt động lực học nói rằng "Các hệ nhiệt động được mô tả đầy đủ bởi các thông số ngoại (hay các thông số quảng tính) và nhiệt độ, 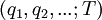$(q_{1},q_{2},...;T)$ ^{[cần dẫn nguồn]}". Nghĩa là một đại lượng bất kỳ đo trên hệ là hàm của thông số ngoại và nhiệt độ. Mặc dù dạng tường minh của các hàm đó là không biết trước, liên hệ giữa chúng cũng như các điều kiện áp đặt lên các hàm đó có thể rút ra từ các nguyên lý của nhiệt động học. Luận điểm xuất phát đó có thể coi như nguyên lý không của nhiệt động học. (đang thảo luận [cmt:])

'"Phát biểu nguyên lý 0"'

Nguyên lý thứ nhất của nhiệt động lực học thiết lập sự tồn tại của nội năng: Với mỗi hệ nhiệt động tồn tại một đại lượng gọi là nội năng là hàm của các thông số ngoại và nhiệt độ , $U(q_{1},q_{2},...;T)$ .

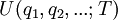"Phát biểu nguyên lý 1"

Nguyên lý thứ hai của nhiệt động lực học thiết lập sự tồn tại của entropy và chiều hướng của quá trình nhiệt.

Các thế nhiệt động.

Cơ sở vật lý thống kê của nhiệt động học

(xem thêm: Vật lý thống kê)

Tài liệu tham khảo

Callen, Thermodynamics.

Bazarov, Nhiệt động lực học.

K. Huang, Statistical Mechanics.

Jaynes...

Ghi chú về hình thức hóa nhiệt động học

Một số khái niệm khá tổng quát có thể dùng để hình thức hóa nhiệt động học, rất tiếc chưa hợp thành một hệ thống (x. ***)

1. Một hệ nhiệt động tồn tại trong một không gian các trạng thái nhiệt động, hay các trạng thái chuẩn cân bằng (về mặt vật lý hệ có những trạng thái không nhiệt động, trạng thái chuẩn cân bằng gồm một số hữu hạn các trạng thái cân bằng). Một đường (x. liên tục đường. S.HUS) nối hai trạng thái bất kỳ của không gian các trạng thái nhiệt động gọi là một quá trình chuẩn cân bằng (chuẩn tĩnh), có thể định nghĩa quá trình nghịch của quá trình chuẩn tĩnh. Công và nhiệt là các phiếm hàm tương ứng mỗi quá trình với mỗi số thực gọi là công và nhiệt lượng. Nguyên lý một nhiệt động học nói rằng hiệu hai phiếm hàm này, gọi là biết thiên nội năng không phụ thuộc vào quá trình có chung điểm đầu và cuối (như vật giới hạn một lớp các hệ, kiểm tra: các hệ trao đổi số hạt có thỏa mãn định nghĩa này hay không?)

2. Một hệ cân bằng (về mặt vật lý là cân bằng nhiệt động học) khi chia thành các hệ con thì các hệ con là cân bằng. Các hệ con của một hệ cân bằng được gọi là cân bằng với nhau. Hai hệ cùng cân bằng với một hệ thì cân bằng với nhau.

3. Trong không gian trạng thái của hệ chuẩn cân bằng tồn tại duy nhất một trạng thái cân bằng (không luôn luôn đúng x. Callen appendix). ĐỊnh nghĩa quá trình tự phát và phát biểu nguyên lý hai?