Thảo luận:Đại số 10/Chương III/§2. Phương trình quy về phương trình bậc nhất, bậc hai

Từ VLOS
Bước tới: chuyển hướng, tìm kiếm

@Xincamonhgvn: cảm ơn bạn, tôi đã sửa lại. Tôi rất vui vì những phản hồi tích cực của bạn cho các bài viết này. Thân mến!

Nguyenthephuc, 01:52, 26/7/2011 (UTC)

VD1-cách giải 2 (bình phương 2 vế của (3) chỉ nhận bậc 2 của x, sao lại có x bậc 3? anh (chị) xem lại dùm!

Xincamonhgvn, 23:09, 25/7/2011 (UTC)

Thời lượng[sửa]

3 tiết = 2 tiết/Lí thuyết + 1 tiết/Bài tập

Chuẩn bị[sửa]

Mục tiêu[sửa]

  • Ôn tập các kiến thức đã học ở lớp 9 về phương trình bậc nhất, bậc hai.
  • Cung cấp cho học sinh cách giải hai loại phương trình quy về bậc nhất, bậc hai: phương trình chứa ẩn trong dấu giá trị tuyệt đối và phương trình chứa ẩn dưới dấu căn thức bậc hai.
  • Giải được các phương trình không quá khó thuộc các loại nói trên.

Nội dung[sửa]

Ôn tập[sửa]

Phương trình quy[sửa]

Có nhiều phương trình khi giải có thể quy về việc giải phương trình bậc nhất hoặc bậc hai như phương trình chứa ẩn ở mẫu thức, phương trình trùng phương, phương trình tích, phương trình chứa ẩn trong dấu giá trị tuyệt đối, phương trình chứa ẩn dưới dấu căn,...

Chương trình THCS đã giới thiệu ba loại phương trình đầu, vì vậy SGK Đại số 10 giới thiệu thêm hai loại sau, viết gọn là phương trình chứa ẩn trong dấu giá trị tuyệt đối và phương trình chứa ẩn dưới dấu căn.

Thực ra, không nhất thiết chỉ phương trình chứa ẩn dưới dấu căn thức bậc hai mới quy được về phương trình bậc hai. Chẳng hạn học sinh lớp 9 đã học căn bậc ba thì phương trình sau cũng có thể quy về phương trình bậc hai.

{\sqrt[ {3}]{x^{3}+x^{2}+3}}=x+1.

Tuy nhiên đối với chương trình GDTHPT môn Toán lớp 10, SGK chỉ nêu ví dụ và bài tập đối với những phương trình chứa ẩn dưới dấu căn thức bậc hai dạng đơn giản.

Phương trình chứa ẩn trong dấu giá trị tuyệt đối[sửa]

Phương pháp giải là khử dấu giá trị tuyệt đối để đưa về một phương trình bậc nhất hoặc bậc hai.

Có hai cách khử dấu giá trị tuyệt đối. Đó là dùng định nghĩa của giá trị tuyệt đối hoặc bình phương hai vế. Với cách thứ hai, có thể dẫn đến việc giải phương trình bậc cao.

Ví dụ: Giải phương trình

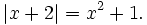
|x+2|=x^{2}+1.

Nếu bình phương hai vế, ta dẫn tới phương trình bậc bốn:

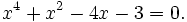
x^{4}+x^{2}-4x-3=0.

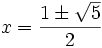Trong khi đó nếu dùng định nghĩa của trị tuyệt đối ta quy về việc giải phương trình bậc hai và được hai nghiệm x={\frac {1\pm {\sqrt {5}}}{2}} .

Phương trình chứa ẩn dưới dấu căn[sửa]

Như đã nêu, nhiều phương trình chứa ẩn dưới dấu căn thức khi giải có thể quy về phương trình bậc hai (hoặc phương trình bậc nhất). Để đơn giản, SGK chỉ nêu ví dụ về phương trình chứa ẩn dưới dấu căn thức bậc hai.

Cách giải loại phương trình này là bình phương hai vế để đưa về một phương trình bậc hai hoặc bậc nhất, tính nghiệm rồi thử vào phương trình ban đầu để loại nghiệm ngoại lai.

Cách giải chung, có thể gồm 4 bước:

  1. Tìm điều kiện
  2. Bình phương hai vế
  3. Kiểm tra điều kiện
  4. Thử lại nghiệm

Như vậy, có thể phân chia các phương trình loại này một cách chi tiết hơn:

  1. Vô nghiệm
  2. Có một nghiệm
  3. Có hai nghiệm

Sơ đồ chi tiết

Tập tin:So do.jpg

Hướng dẫn giải bài tập[sửa]

Các bài tập gồm hai loại: phần ôn và phần mới.

Các bài ôn gồm 4 bài: từ 1 đến 4 theo các chủ đề giải và biện luận phương trình bậc nhất, giải bài toán bằng cách lập phương trình và phương trình trùng phương. Tùy theo tình hình thực tế của lớp, giáo viên có thể yêu cầu làm một số trong các bài này để ôn tập lại kĩ năng giải toán. Bài tập số 5 rèn luyện cho học sinh sử dụng máy tính bỏ túi để giải các phương trình bậc hai.

Hai bài tập 6 và 7 ứng dụng với hai dạng mới. Chú ý rằng các tam thức trong câu 7c và 7d luôn luôn dương.

Lấy từ “https://tusach.thuvienkhoahoc.com/index.php?title=Thảo_luận:Đại_số_10/Chương_III/§2._Phương_trình_quy_về_phương_trình_bậc_nhất,_bậc_hai&oldid=83051”