Chủ đề nóng: Phương pháp kỷ luật tích cực - Cổ học tinh hoa - Những thói hư tật xấu của người Việt - Công lý: Việc đúng nên làm - Giáo án Điện tử - Sách giáo khoa - Học tiếng Anh - Bài giảng trực tuyến - Món ăn bài thuốc - Chăm sóc bà bầu - Môi trường - Tiết kiệm điện - Nhi khoa - Ung thư - Tác hại của thuốc lá - Các kỹ thuật dạy học tích cực
- Dạy học phát triển năng lực - Chương trình giáo dục phổ thông
Kinh nghiệm dạy học/Chống chủ nghĩa hình thức trong dạy và học toán
Từ VLOS
Chống chủ nghĩa hình thức trong dạy và học toán
Diễn đạt bằng lời/ý nghĩa[sửa]
Một cách để "học sinh hiểu được bản chất các kiến thức" là yêu cầu học sinh phát biểu/diễn đạt các công thức/phương trình ... bằng lời.
- Ví dụ
-
Định
lý
Pitago
trong
tam
giác
vuông
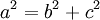 :
trong
tam
giác
vuông,
tổng
bình
phương
một
cạnh
bằng
tổng
bình
phương
hai
cạnh
còn
lại.
Ngược
lại,
một
tam
giác
có
bình
phương
một
cạnh
bằng
tổng
bình
phương
hai
cạnh
còn
lại
thì
tam
giác
đó
vuông
:
trong
tam
giác
vuông,
tổng
bình
phương
một
cạnh
bằng
tổng
bình
phương
hai
cạnh
còn
lại.
Ngược
lại,
một
tam
giác
có
bình
phương
một
cạnh
bằng
tổng
bình
phương
hai
cạnh
còn
lại
thì
tam
giác
đó
vuông -
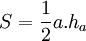 :
diện
tích
tam
giác
bằng
một
nửa
tích
đường
cao
nhân
với
cạnh
đáy
tương
ứng
:
diện
tích
tam
giác
bằng
một
nửa
tích
đường
cao
nhân
với
cạnh
đáy
tương
ứng -
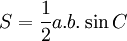 :
diện
tích
tam
giác
bằng
một
phần
hai
tích
hai
cạnh
nhân
với
sin
của
góc
xen
giữa.
:
diện
tích
tam
giác
bằng
một
phần
hai
tích
hai
cạnh
nhân
với
sin
của
góc
xen
giữa. -
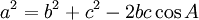 :
trong
một
tam
giác,
bình
phương
một
cạnh
bằng
tổng
bình
phương
hai
cạnh
còn
lại
trừ
đi
hai
lần
tích
hai
cạnh
đó
với
cosin
góc
đối
diện
(góc
xen
giữa)
hoặc
trong
một
tam
giác
biết
hai
cạnh
và
một
góc
ta
tìm
được
cạnh
thứ
ba.
:
trong
một
tam
giác,
bình
phương
một
cạnh
bằng
tổng
bình
phương
hai
cạnh
còn
lại
trừ
đi
hai
lần
tích
hai
cạnh
đó
với
cosin
góc
đối
diện
(góc
xen
giữa)
hoặc
trong
một
tam
giác
biết
hai
cạnh
và
một
góc
ta
tìm
được
cạnh
thứ
ba. -
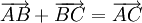 -
tổng
hai
vecto
nối
tiếp
là
một
vecto
có
điểm
đầu
là
điểm
đầu
của
vecto
thứ
nhất
và
điểm
cuối
là
điểm
cuối
của
vecto
thứ
hai
-
tổng
hai
vecto
nối
tiếp
là
một
vecto
có
điểm
đầu
là
điểm
đầu
của
vecto
thứ
nhất
và
điểm
cuối
là
điểm
cuối
của
vecto
thứ
hai -
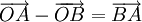 -
hiệu
hai
vecto
có
cùng
điểm
đầu
là
một
vecto
có
điểm
đầu
là
điểm
cuối
của
vecto
thứ
hai
và
điểm
cuối
là
điểm
đầu
của
vecto
thứ
nhất
(nôm
na:
điểm
đầu
là
điểm
cuối,
điểm
cuối
là
điểm
đầu)
-
hiệu
hai
vecto
có
cùng
điểm
đầu
là
một
vecto
có
điểm
đầu
là
điểm
cuối
của
vecto
thứ
hai
và
điểm
cuối
là
điểm
đầu
của
vecto
thứ
nhất
(nôm
na:
điểm
đầu
là
điểm
cuối,
điểm
cuối
là
điểm
đầu) -
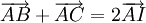 -
tổng
hai
vecto
có
cùng
điểm
đầu
bằng
2
lần
vecto
trung
tuyến
(chưa
được
chính
xác
nhưng
dễ
nhớ);
-
tổng
hai
vecto
có
cùng
điểm
đầu
bằng
2
lần
vecto
trung
tuyến
(chưa
được
chính
xác
nhưng
dễ
nhớ); -
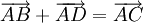 -
tổng
hai
vecto
xuất
phát
từ
một
đỉnh
là
một
vecto
cũng
xuất
phát
từ
đỉnh
đó
...
-
tổng
hai
vecto
xuất
phát
từ
một
đỉnh
là
một
vecto
cũng
xuất
phát
từ
đỉnh
đó
... -
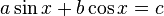 -
phương
trình
bậc
nhất
hai
hàm
sin
và
cos
của
cùng
một
góc
-
phương
trình
bậc
nhất
hai
hàm
sin
và
cos
của
cùng
một
góc
Vận dụng linh hoạt[sửa]
Thông thường SGK chỉ giới thiệu một cách viết các công thức/đẳng thức/phương trình, giáo viên cần giúp học sinh phát hiện và vận dụng các công thức/phương trình đó ở những dạng khác (chiều thuận, chiều ngược,...)
- Ví dụ
-
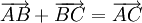
TH khác: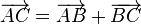
-
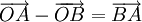
TH khác: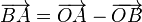
-
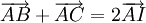
TH khác: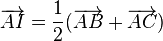
-
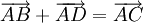
TH khác: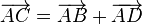
-
SGK:
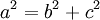
TH khác: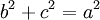
-
SGK:
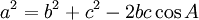
TH khác: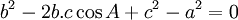
-
SGK:
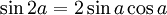
TH khác: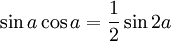 ;
;
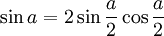
-
SGK:
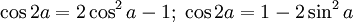
TH khác: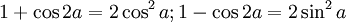
- Dạy học Công thức nhân đôi
Công
thức
nhân
đôi:
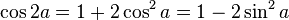
Hỏi:
Áp
dụng
công
thức
nhân
đôi
cho
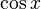 ta
được?
ta
được?
Trả
lời:
ta
được
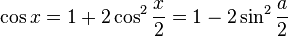
Xem thêm[sửa]
- Dạy và kiểm tra kiến thức học sinh theo lối “học để hiểu”
- Làm sao để học sinh hiểu được bản chất các kiến thức

