Một số điều nên và không nên trong giảng dạy toán/9
Nên:
Làm
sao
cho
học
sinh
hiểu
được
bản
chất
các
kiến
thức
Không
nên:
Lạm
dụng
ngôn
ngữ
hình
thức,
và
dạy
một
cách
giáo
điều
Nên:
Cho
các
bài
tập
nhằm
giúp
học
sinh
nắm
được
bản
chất
của
các
lý
thuyết
đang
học
hoặc/và
luyện
được
các
kỹ
năng
liên
quan
trực
tiếp
Không
nên:
Cho
nhiều
bài
“lạc
đề”,
ít
liên
quan
trực
tiếp
đến
lý
thuyết
đang
học,
đòi
hỏi
mẹo
mực
hoặc
những
lý
thuyết
chưa
được
học
đến.
Tôi sẽ lấy chương trình toán đại số lớp 7, và quyển sách “Các bài toán hay và khó / Đại số lớp 7” của hai tác giả Phan Văn Đức và Nguyễn Hoàng Khanh, xuất bản năm 2003, sau đây gọi tắt là sách BTĐS7, để làm ví dụ minh họa cho phần này. Tôi xin lỗi hai tác giả trên là đã mạn phép đem quyển sách BTĐS7 ra đây “mổ xẻ”. Tôi không có ý chê bai hay công kích gì ai – theo tôi hiểu thì quyển sách này cũng không kém gì các sách toán phổ thông khác đang được dùng ở VN – mà do quyển sách này nó “có số” rơi vào tay tôi trung lúc tôi đang muốn bàn về phương pháp giảng dạy toán.
Thế nào là “giáo điều”? Là dạy một cách áp đặt, đưa ra các thứ như là “chân lý duy nhất”, mà không giải thích vì sao nó như vậy, nó dựa trên cái gì, và không hề nói đến các khả năng khác, các “chân lý” khác. Sự nguy hiểm của lối dạy và học theo kiểu giáo điều, là biến học sinh thành những con người thụ động, mất khả năng suy nghĩ một cách độc lập, trở thành “cuồng tín” chấp nhận các thứ như là chân lý mà không đặt câu hỏi “tại sao”, và khi sai thì không biết đâu mà sửa vì “mất gốc”.
Một ví dụ đặc trưng của “văn hóa giáo điều” là môn “Tử vi đẩu số” ở Việt Nam. Các sách viết về tử vi mà tôi được nhìn thấy đều rất giáo điều, cái gì cũng do “Thánh bảo”, không có giải thích tại sao, và tất nhiên nếu xem bị sai thì chỉ còn cách “kêu trời”, không thể biết vì sao sai, sai ở đâu. Mà chắc chắn là dễ sai. Ví dụ, “giờ Tý” thực ra không bắt đầu lúc 11h đêm, mà cách đó khoảng 20 phút (tùy từng ngày), nhưng điều này chỉ có một nhóm nhỏ “thầy tử vi” biết còn có đọc sách cũng không học được. Nếu tìm hiểu kỹ hơn, thì sẽ thấy việc xác định “giờ” đó thực ra ứng với khái niệm Ascendant trong thiên văn học, và có thể tính chính xác “giờ Tý” đến từng giây một bằng các chương trình máy tính cho thiên văn. Hầu hết các “sao” trong tử vi đẩu số là “virtual stars” chứ không phải “sao thật” (nói về mặt toán học, nó có thể coi là một “spectral decomposition” tính ra từ vị trí của 3 điểm: mặt trăng, mặt trời và ascendant trên vòng hoàng đạo?). Cái “spectral decomposition” này trong tử vi đẩu số có lẽ là một phát minh rất lớn, nhưng rất tiếc là không có sách nào giải thích vì sao lại làm như vậy, và qui tắc xếp sao được đưa ra một cách hoàn toàn thần bí . Ở phương Tây cũng có “Tử vi”, gọi là astrology (chiêm tinh học). Tử vi đẩu số và astrology có cùng gốc thiên văn học, và có rất nhiều cái chung. Nhưng khác nhau ở chỗ astrology không giáo điều, mọi thứ có giải thích vì sao, tuy rằng các giải thích đó chưa “đạt mức khoa học”, nhưng cho phép người ta suy nghĩ, kiểm nghiệm, phát triển, sửa sai!
Trở lại toán đại số lớp 7. Tôi đọc quyển BTĐS7 thấy có một số điểm hình thức, giáo điều. Hai ví dụ:
- §11 Chương 1 (Số vô tỉ – Khái niệm về căn bậc hai, trang 22). Tóm tắt lý thuyết của phần này được viết như sau:
-
Số
vô
tỉ
là
số
được
viết
dưới
dạng
số
thập
phân
vô
hạn
không
tuần
hoàn.
- Tập hợp các sô vô tỉ được ký hiệu là I
-
Căn
bậc
hai
của
một
số
a
không
âm
là
số
x
sao
cho
x^2
=
a
-
Số
dương
a
có
đúng
2
căn
bậc
hai:
một
số
dương
ký
hiệu
là
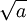 ,
một
số
âm
ký
hiệu
là
,
một
số
âm
ký
hiệu
là
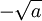
-
Số
0
chỉ
có
một
căn
bậc
hai
là
số
0
viết
là
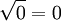
-
Số
dương
a
có
đúng
2
căn
bậc
hai:
một
số
dương
ký
hiệu
là
Đâu là những thứ hình thức, giáo điều trong các câu trên?
Tôi làm toán mấy chục năm nay, chưa bao giờ phải dùng đến ký hiệu “tập hợp các số vô tỉ”, và đến khi đọc sách này tôi mới biết “tập hợp các sô vô tỉ được ký hiệu là I”! Đấy là một “kiến thức” hình thức không dùng để làm gì cả. Và tại sao tôi lại phải ký hiệu nó là I? Tôi muốn dùng ký hiệu khác thì sao?
Câu
“số
vô
tỉ
là
số
được
viết
dưới
dạng
số
thập
phân
vô
hạn
không
tuần
hoàn”
tuy
đúng
về
mặt
hình
thức
toán
học,
nhưng
rất
rắm
rối
khó
hiểu.
Bản
chất
của
“vô
tỉ”
là
“không
hữu
tỉ”,
tức
là
các
số
thực
không
viết
được
dưới
dạng
phân
số.
Để
hình
dung
các
số
vô
tỉ,
cần
làm
bài
tập
ví
dụ
như
“số
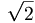 là
số
vô
tỉ”.
là
số
vô
tỉ”.
Hai khái niệm “số vô tỉ” và “căn bậc hai” là hai khái niệm quan trọng, cần có thời gian để hiểu từng khái niệm, không hiểu sao lại được dồn vào chung một mục, cứ như là căn bậc hai của một số thì là số vô tỉ!
Có
ai
nói
“căn
bậc
hai
của
4
là
-2
không”?
Không
ai
nói
thế
cả,
mà
người
ta
chỉ
nói
“căn
bậc
hai
của
4
là
2”.
Tức
là
căn
bậc
hai
của
một
số
thực
dương
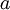 ,
luôn
được
hiểu
là
số
thực
dương
có
bình
phương
bằng
số
kia,
và
ký
hiệu
là
,
luôn
được
hiểu
là
số
thực
dương
có
bình
phương
bằng
số
kia,
và
ký
hiệu
là
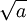 .
Bản
thân
cái
ký
hiệu
.
Bản
thân
cái
ký
hiệu
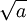 được
đọc
là
“căn
bậc
hai
của
a”
(“square
root
of
a”
tiếng
Anh).
Việc
dạy
cho
học
trò
là
“a
có
2
căn
bậc
2”
tuy
có
thể
đúng
về
hình
thức,
nhưng
rắm
rối,
và
thực
ra
chỉ
“đúng
nửa
vời”.
Nếu
một
số
có
2
căn
bậc
hai,
thì
cũng
phải
có
3
căn
bậc
ba,
nhưng
giải
thích
với
học
sinh
lớp
7
chuyện
một
số
có
3
căn
bậc
3
sao
đây?
Nói
là
phương
trình
được
đọc
là
“căn
bậc
hai
của
a”
(“square
root
of
a”
tiếng
Anh).
Việc
dạy
cho
học
trò
là
“a
có
2
căn
bậc
2”
tuy
có
thể
đúng
về
hình
thức,
nhưng
rắm
rối,
và
thực
ra
chỉ
“đúng
nửa
vời”.
Nếu
một
số
có
2
căn
bậc
hai,
thì
cũng
phải
có
3
căn
bậc
ba,
nhưng
giải
thích
với
học
sinh
lớp
7
chuyện
một
số
có
3
căn
bậc
3
sao
đây?
Nói
là
phương
trình
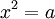 có
hai
nghiệm
thực
có
hai
nghiệm
thực
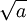 và
và
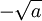 khi
khi
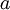 là
số
dương
thì
đúng
bản
chất
hơn.
là
số
dương
thì
đúng
bản
chất
hơn.
Để
hiểu
được
căn
bậc
hai,
một
cách
tốt
nhất
là
làm
ví
dụ,
như
là
tính
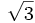 chính
xác
đến
3-4
chữ
số
(mà
không
dùng
máy
tính).
Tôi
có
thí
nghiệm
dạy
cho
con
tôi
(lúc
quãng
9-10
tuổi)
tính
chính
xác
đến
3-4
chữ
số
(mà
không
dùng
máy
tính).
Tôi
có
thí
nghiệm
dạy
cho
con
tôi
(lúc
quãng
9-10
tuổi)
tính
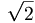 ,
rồi
sau
đó
nó
tự
tính
,
rồi
sau
đó
nó
tự
tính
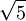 ,
mất
khá
nhiều
thời
gian
và
viết
mất
mấy
trang
giấy,
nhưng
nó
tính
được,
và
qua
đó
không
những
hiểu
được
thế
nào
là
căn
bậc
hai,
mà
còn
hiểu
được
phương
pháp
tính
gần
đúng
nó
như
thế
nào,
qua
ví
dụ
cụ
thể.
Trong
sách
BTĐS7
có
những
bài
tập
có
thể
coi
là
rất
khó
(vượt
xa
mức
chương
trình?)
trong
đó
có
căn
bậc
hai
,
mất
khá
nhiều
thời
gian
và
viết
mất
mấy
trang
giấy,
nhưng
nó
tính
được,
và
qua
đó
không
những
hiểu
được
thế
nào
là
căn
bậc
hai,
mà
còn
hiểu
được
phương
pháp
tính
gần
đúng
nó
như
thế
nào,
qua
ví
dụ
cụ
thể.
Trong
sách
BTĐS7
có
những
bài
tập
có
thể
coi
là
rất
khó
(vượt
xa
mức
chương
trình?)
trong
đó
có
căn
bậc
hai
(ví
dụ
bài
95b:
chứng
minh
rằng
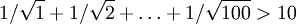 ),
),
mà
lại
thiếu
những
bài
“đơn
giản”
nhưng
giúp
hiểu
bản
chất
của
căn
bậc
hai,
như
bài
“tính
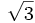 chính
xác
đến
3
chữ
số
sau
dấu
phẩy”
như
tôi
viết
phía
trên.
chính
xác
đến
3
chữ
số
sau
dấu
phẩy”
như
tôi
viết
phía
trên.
- §3 Chương 3 (phần Biểu Đồ, chương Thống Kê, trang 114 của sách BTĐS) có viết:
Ngoài bảng số liệu thống kê ban đầu, bảng “tần số”, người ta còn dùng biểu đồ để cho một hình ảnh cụ thể về giá trị của dấu hiệu và tần số.
Có các loại biểu đồ như sau: biểu đồ đoạn thẳng, biểu đồ hình chữ nhật, biểu đồ hình quạt.
Vì sao những câu trên là giáo điều? Vì nó ép đặt (chỉ có 3 loại biểu đồ, và nói là biểu đồ “cho một hình ảnh cụ thể”). Ý nghĩa của biểu đồ được giải thích không chính xác (thế nào là “hình ảnh cụ thể”? Thực ra biểu đồ hoàn toàn có thể “kém cụ thể, kém chính xác” hơn là các số, nhưng nó cho một bức tranh trực giác, giúp cho người đọc nắm được thông tin quan trọng một cách nhanh chóng bằng hình ảnh). Ý nghĩa của biểu đồ nằm ở chỗ nó cho phép người đọc dùng bộ phận “xử lý hình ảnh” của não để nạp và xử lý thông tin – bộ phận đó của não người “chạy” nhanh hơn nhiều so với bộ phận “xử lý số”, và như vậy các thông tin ở dạng biểu đổ có thể được đọc nhanh hơn nhiều lần là ở dạng số (tuy rằng với độ chính xác có thể thấp hơn). Và tại sao lại chỉ có 3 dạng biểu đồ? Điều này hoàn toàn sai thực tế! Các dạng biểu đồ là do con người nghĩ ra, và người ta có thể nghĩ ra một tỷ dạng khác nhau. Tuy rằng 3 dạng trên có thể là 3 dạng hay gặp nhất (một phần lý do là do nó đơn giản, dễ vẽ), nhưng không phải là không có các dạng khác, cũng khá phổ biến trong những tình huống nào đó. Ví dụ như biểu đồ dùng màu (màu xanh chỉ đi lên, màu đỏ chỉ đi xuống, xanh đậm là lên cao ..., không cần nhìn số mà chỉ cần nhìn bảng các màu sắc là hình dung được sự thay đổi) khá thuận tiện cho việc xem sự thay đổi của giá cả trên thị trường chứng khoán. Hay biểu đồ dùng bản đồ thế giới (ở trên mỗi nước có một khoanh tròn hay khoanh vuông nào đó, to nhỏ phụ thuộc vào số lượng một cái gì đó ở nước đó to hay nhỏ) là những biểu độ địa lý rất hữu ích, v.v. Những biểu đồ như vậy là những biểu đồ thống kê gặp trong thực tế, chứ không phải chỉ có 3 loại biểu đồ như trong “sách bảo”.
Nhân tiện nói thêm: tất nhiên, lý thuyết thống kê dạy cho học sinh lớp 7 khá sơ sài. Tôi không rõ mục đích dạy thống kê ở lớp 7 để làm gì, trong khi chưa đủ cơ sở toán để học nhập môn “thống kê toán học” theo đúng nghĩa, chứ không dừng lại ở chỗ “đếm xem giá trị x xuất hiện mấy lần trong một bảng” (là thứ “trivial” không cần phải dạy, bất cứ ai khi gặp câu hỏi như vậy và hiểu câu hỏi trong tình huống cụ thể đều đếm được dễ dàng). Ngay 1 khái niệm rất dễ hiểu và rất cơ bản của thống kê là “median value” (giá trị giữa? - ví dụ như khi nói đến mức lương tiêu biểu của một nghề nào đó người ta thường dùng mức median chứ không phải average) cũng không thấy có trong sách lớp 7. Dạy “tủn mủn” có một tẹo về thống kê, không thành một thứ “coherent”, không hiểu ý nghĩa và công dụng, thì khó “đọng” được.
Nói thêm về bài tập. Thế nào là một bài tập hay? Theo tôi một bài tập hay là một bài tập “đặt đúng chỗ, đúng mục đích”, giúp học sinh nắm được phần lý thuyết đang cần nắm hoặc là rèn được kỹ năng đang cần rèn, hoặc là (trong trường hợp kiểm tra thi cử) kiểm tra được đúng những kiến thức và kỹ năng cần kiểm tra. Cùng là một bài tập, nhưng có thể hay trong tình huống này, lại trở thành không hay trong tình huống khác, nếu bị “đặt nhầm chỗ”. Trong quyển sách BTĐS7, gọi là “Những bài toán khó và hay”, tôi thấy có những bài tuy khó thì có thể khó thật, nhưng “hay” thì tôi “không thấy hay”, bởi vì dường như chúng bị “đặt nhầm chỗ”. Chúng giống như những bài toán đánh đố, mẹo mực, hơn là những bài toán liên quan trực tiếp đến phần kiến thức ký thuyết trong chương trình mà học sinh cần nắm vững.
Ví dụ: Chương 1, về “số hữu tỷ và số vô tỷ”. Theo tôi hiểu, mục đích của chương này là cho học sinh biết làm các phép tính với các số hữu tỷ (tức là các phân số), và hiểu được rằng có những số vô tỷ, đồng thời biết được khái niệm thế nào là căn bậc hai của một số. Chương này không nhằm dạy về vấn đề vấn đề chia hết trong số học, hay về tính toán các biểu thức đại số phức tạp. Thế nhưng trong Chương 1 có bài tập sau: Chứng minh rằng A = 75. (4^1999 + 4^1998 + ... + 4 + 1) + 25 chia hết cho 100. Để làm được bài này, học sinh cần biết cách cộng 4^1999 + 4^1998 + ... + 4 + 1 (là một bài toán có thể coi là khó đối với học sinh lớp 7?, tuy nhiên nó không phải là mục đích kiến thức của chương), rồi sau đó kiểm tra sự chia hết cho 100, cũng không phải là cái nằm trong kiến thức mà Chương 1 này muốn học sinh nắm được. Một bài toán như vậy, dù dễ hay khó, cũng không hay, vì “nhầm chỗ”.
Ví dụ khác: trong Chương 1 có những bài tập về bất đẳng thức (như bài 95) hay cực trị (như bài 125) là những bài khó. Nó khó vì học sinh không được học tý gì về lý thuyết (phương pháp đánh giá các đại lượng hay tìm cực trị) mà phải làm bài tập. Nếu làm bài tập, mà không có phương pháp làm, tức là “đoán mò”, có nghĩa là sẽ làm một cách mẹo mực. Nó có thể coi là bài hay, nếu xếp vào dạng “toán đố nhằm rèn luyện tư duy, khả năng suy luận sâu cho học sinh giỏi” (tức là cho một tỷ lệ nhỏ học sinh có óc tò mò đặc biệt về toán), nhưng nó không “hay” nếu đấy là bài tập để học về “số hữu tỉ và vô tỉ”. Một học sinh “bình thường”, nếu gặp những bài như vậy khó có thể làm được (họ nghĩ một lúc không ra sẽ thấy chán và tự hỏi “tại sao phải làm bài như vậy”), dù đã tính toán thành thạo với các phân số và biết tính căn bậc hai. Nhưng nếu được học về các phương pháp tìm cực trị hay đánh giá các đại lượng rồi, thì mấy bài toán đó không còn gì “khó”, có điều mấy phương pháp đó lại không có trong chương trình chính thức! Tôi e rằng kiểu “đánh đố” như vậy sẽ làm cho nhiều học sinh lầm tưởng rằng họ dốt, không học được toán, trong khi thực ra họ có thể học, hiểu và dùng được các công cụ toán rất hiệu quả, nếu được dạy “bài bản” hơn. Không hiểu kiểu “toán đố” này có phải một trong những nguyên nhân khiến học sinh phải đi học thêm tràn lan đến tối mịt không? (Nếu không học thêm thì “làm sao mà giải được bài tập”!).
(DRAFT 14/07/2009)
Nguồn[sửa]
- http://zung.zetamu.com/?p=1000
- Tác giả đã cho phép đăng lại trên VLOS (chi tiết).
<< trang trước
>> trang sau
Ý kiến của bạn[sửa]
Bài liên quan
Liên kết đến đây
- Một số điều nên và không nên trong giảng dạy toán/8
- Một số điều nên và không nên trong giảng dạy toán/10
- Một số điều nên và không nên trong giảng dạy toán/11
- Thành viên:Nguyenthephuc/Note: Chống chủ nghĩa hình thức trong dạy và học toán
- Kinh nghiệm dạy học/Chống chủ nghĩa hình thức trong dạy và học toán


