Thành viên:Nguyenthephuc/Note: Đại số 11/Hàm số lượng giác

Từ VLOS
Bước tới: chuyển hướng, tìm kiếm

Mục tiêu[sửa]

Giúp HS:

  • Nắm được cách xác định các hàm số lượng giác y = sin x, y = cos x, y = tan x, y = cot x trong đó x là số đo radian của góc lượng giác
  • Nắm được các tính chất đơn giản (tập xác định, tính chất chẵn lẻ, đặc biệt tính chất tuần hoàn của các hàm số nói trên)
  • Biết cách dựa vào chuyển động của điểm trên đường tròn lượng giác và trên các trục sin, cosin, tang và cotang để khảo sát sự biến thiên của các hàm số nói trên[1]
  • Nhận biết được dạng đồ thị của hàm số đó

Chuẩn bị của học sinh[sửa]

Kiến thức

  • Khái niệm hàm số đồng biến (biến tăng hàm tăng, biến giảm hàm giảm) và nghịch biến (biến tăng hàm giảm, biến giảm hàm tăng)
  • Mối quan hệ giữa chiều biến thiên và đồ thị của hàm số (đồng biến ~ nét đi lên; nghịch biến ~ nét đi xuống)
  • Hàm số chẵn, lẻ
  • Giá trị lượng giác của hai cung đối nhau, hơn kém π và hơn kém 2π
  • Giá trị lớn nhất, giá trị nhỏ nhất của sin và cos

Kĩ năng

  • Biểu diễn cung lượng giác trên đường tròn lượng giác (xác định điểm cuối)
  • Biểu diễn giá trị lượng giác trên trục lượng giác với cung cho trước.
  • Biểu diễn chiều biến thiên bằng bảng biến thiên
  • Đọc chiều biến thiên từ đồ thị

Dụng cụ học tập

  • Thước thẳng, compa (vẽ bảng biến thiên, đồ thị, đường tròn)
  • Máy tính (tính giá trị gần đúng giá trị lượng giác để vẽ đồ thị)

Chú thích[sửa]

  1. ↑ Cách suy đoán chiều biến thiên của hàm số lượng giác nhờ đường tròn lượng giác và trục lượng giác. (Bằng cách theo dõi: chuyển động của chất điểm trên đường tròn lượng giác, giá trị của cung lượng giác trên đường tròn lượng và giá trị của hàm số trên trục lượng giác tương ứng; từ đó thấy được mối quan hệ về biến thiên (cùng tăng/giảm) giữa đối số và hàm số mà suy đoán về chiều biến thiên của hàm số) - Đây tri thức phương pháp, nó thật sự quan trọng hơn nhiều so với bản thân kiến thức về chiều biến thiên. Nhờ nó học sinh có thể biết được chiều biến thiên của những hàm số lượng giác mở rộng từ các hàm sin, cos, tan, cot như 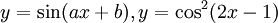y=\sin(ax+b),y=\cos ^{2}(2x-1) , ... Hơn nữa, xét trong toàn bộ chương trình học thì kiến thức này càng quan trọng - cái mà học sinh sẽ phải vận dụng nhiều trong các bài toán thay vì nhớ các hàm số sin, cos,... đồng biến, nghịch biến khi nào

Tham khảo[sửa]

Liên kết đến đây

Lấy từ “https://tusach.thuvienkhoahoc.com/index.php?title=Thành_viên:Nguyenthephuc/Note:_Đại_số_11/Hàm_số_lượng_giác&oldid=83844”