Thành viên:Nguyenthephuc/Note: So sánh điểm kì thi tốt nghiệp trung học của Hà Giang và cả nước

Mấy ngày qua, dự luận công chúng ngạc nhiên và đặt dấu hỏi về kì thi tốt nghiệp trung học phổ thông liên quan đến môn toán và Hà Giang. Tôi thử xem qua bằng số liệu thực tế thì quả thật là đáng nghi ngờ. Hai câu hỏi đặt ra là:

(a) Theo kết quả công bố năm nay thì có 951 thí sinh có điểm 0 môn toán. Câu hỏi là số thí sinh có điểm 0 môn toán như vậy là bất bình thường;

(b) phân bố điểm thi của thí sinh Hà Giang có khác biệt một cách đáng chú ý so với phân bố của cả nước.

Tôi may mắn được một bạn đọc cung cấp toàn bộ số liệu điểm thi CỦA MỖI THÍ SINH cho mỗi môn thi trên cả nước và cho tỉnh Hà Giang. Dung lượng data lên đến 50 MB. Đây là dữ liệu rất quí. Dựa vào dữ liệu này, tôi có thể trả lời hai câu hỏi cụ thể hơn.

Trả lời câu hỏi thứ nhất thì dễ với xác suất. Môn toán có 50 câu, mỗi câu có 4 lựa chọn. Do đó, xác suất sai cho mỗi câu hỏi là 3/4. Xác suất một thí sinh sai tất cả 50 câu phải là p = (3/4)^50 = 0.0000005663 (giả định độc lập). Nhưng ở đây, chúng ta có n=917484 thí sinh. Gọi x là số thí sinh có điểm 0, lí thuyết phân bố nhị phân cho biết giá trị trung bình của x là mean(x) = np = 0.51 và độ lệch chuẩn sd = sqrt(n*p*(1-p)) = 0.72. Dùng hai tham số này để mô phỏng thì chúng ta có thể tính xác suất có 951 thí sinh có điểm 0:

1-pnorm(951, mean=0.51, sd=0.72) kết quả là 0. Một cách khác là giá trị kì vọng trong số 1 triệu thí sinh thi, thì tối đa chỉ có 3 thí sinh với điểm 0 môn toán. Nhưng trong thực tế, kì thi này ghi nhận có đến 951 thí sinh có điểm 0. Và, đó là điều bất thường.

Phân tích mô tả

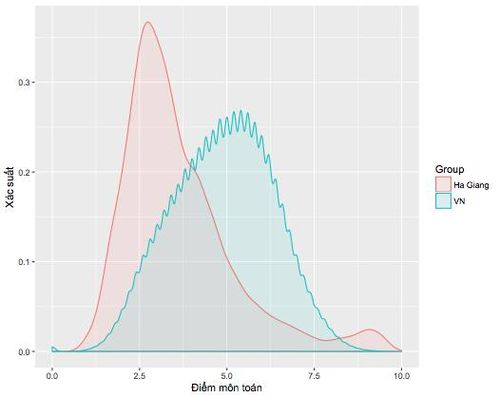
Trả lời câu hỏi 2 nhiêu khê hơn một chút. Cách đơn giản nhất là qua biểu đồ phân bố. Biểu đồ dưới đây (Hình 1) cho thấy phân bố điểm của Hà Giang (màu hồng) và của cả nước (màu xanh). Có hai điểm chính có thể rút ra từ hình này:

Hình 1: Biểu đồ phân bố điểm môn toán cho Hà Giang (màu hồng) và cả nước (màu xanh). Chú ý phần nhô lên ở nóm điểm cao (trên 8.6) của Hà Giang!

(a) Điểm trung vị của Hà Giang là khoảng 3.2, thấp hơn điểm của toàn quốc (trung vị khoảng 5.0);

(b) Phân bố điểm của Hà Giang có vẻ bất thường ở điểm từ 8 đến 10. Chú ý đường biểu diễn "nhô lên" trong khi đáng lí ra phải smooth như cả nước.

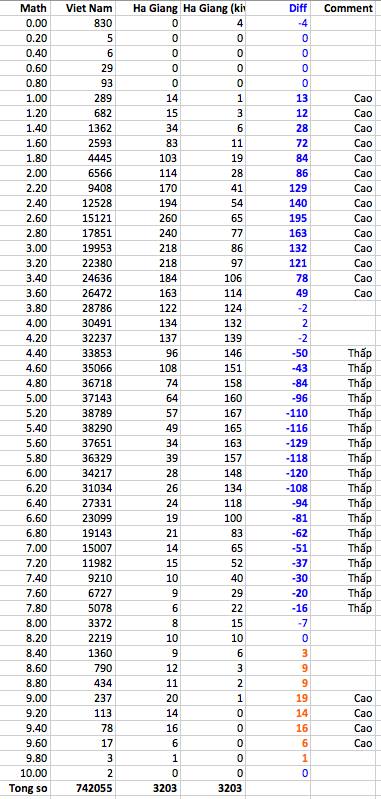
Để kiểm tra kĩ hơn chỗ "nhô lên" đó, cần phải phân tích so sánh giữa phân bố điểm của Hà Giang và điểm của cả nước (Hình 2, bảng số liệu).

• Bước 1: tìm phân bố của cả nước. Nói cách khác, đếm số thí sinh có điểm 0, 0.2, 0.4, 0.6,..., 10. Cột 2 của hình sau đây thể hiện kết quả đó.
• Bước 2: tìm phân bố của Hà Giang. Đếm số thí sinh có điểm 0, 0.2, 0.4, 0.6,..., 10. Hà Giang có 3203 thí sinh. Cột 3 của hình sau đây thể hiện kết quả cho Hà Giang.
• Buớc 3: tính giá trị kì vọng cho Hà Giang. Chúng ta hỏi: nếu phân bố điểm thi của cả nước (bước 1) áp dụng cho Hà Giang thì có bao nhiêu em có điểm 0, 0.2, 0.4, 0.6,..., 10. Tạm gọi đây là điểm kì vọng. Kết quả được trình bày trong cột 4.
• Bước 4: ở mỗi điểm, lấy số thí sinh Hà Giang thực tế đạt được trừ cho số [kì vọng] thí sinh mà nếu phân bố của cả nước. Cột 5 trình bày kết quả này.

Hình 2: So sánh phân bố điểm thi môn toán giữa cả nước (cột 2) và Hà Giang (cột 3). Cột 4 thể hiện số thí sinh mà "đáng lẽ" Hà Giang sẽ có nếu điểm thi ở đây giống như cả nước. Cột 5 thể hiện mức độ khác biệt (hay chênh) giữa số thí sinh thực tế và số thí sinh kì vọng.

Dĩ nhiên, nếu phân bố điểm thi của Hà Giang tương đương với phân bố của cả nước, thì cột thứ 5 sẽ gần bằng 0. Nhưng chúng ta thấy trong thực tế thì không phải vậy, và vài chỗ lệch thể hiện rất rõ sau đây:

(a) Ở điểm thấp (từ 1 đến 3.6), số thí sinh Hà Giang cao hơn so với giá trị kì vọng;

(b) Nhưng ở điểm cao hơn (từ 4.0 đến 7.8) thì số thí sinh Hà Giang thấp hơn giá trị kì vọng của cả nước;

(c) Nhưng điều thú vị nhất là ở điểm cao 'top' (từ 8.6 đến 9.6) số thí sinh Hà Giang cao hơn so với phân bố cả nước. Nếu theo xu hướng của cả nước, Hà Giang chỉ có 7 thí sinh ở ngưỡng điểm 8.6 đến 9.6, nhưng trong thực tế con số thí sinh đạt điểm này là 72, tức cao gấp ~10 lần so với cả nước!

Phân tích tương quan

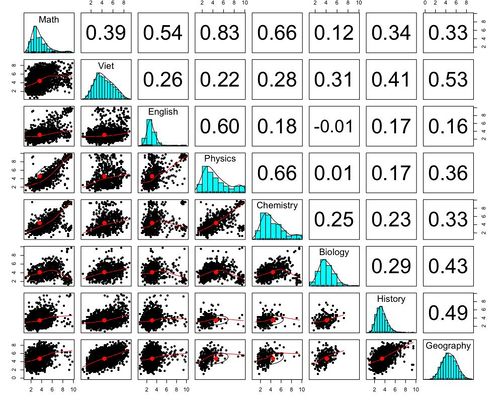
Một cách khác để biết sự bất bình thường ở Hà Giang là qua phân tích tương quan. Nếu chúng ta lấy mối tương quan về điểm giữa các môn học của các nước (Hình 3) làm 'chuẩn', và so sánh hệ số tương quan với tỉnh Hà Giang (Hình 4) là sẽ thấy vài bất bình thường. Chẳng hạn như hệ số tương quan giữa môn toán và sinh học của cả nước là 0.36, nhưng ở Hà Giang hệ số này chỉ 0.12! Đó cũng là một tín hiệu bất bình thường.

Hình 3: Hệ số tương quan (đo lường mức độ tương quan) giữa các môn học cho cả nước. Số liệu được tính trên 917484 thí sinh.
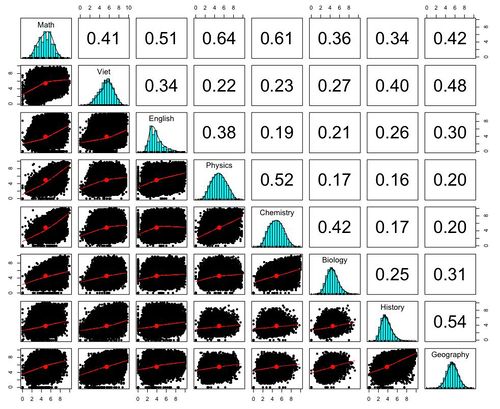
Hệ số tương quan gần bằng 1 có nghĩa là "chặt chẽ", gần bằng 0 có nghĩa là không có tương quan. Chú ý tất cả hệ số tương quan đều khá thấp, nói lên rằng thí sinh có khi giỏi môn toán nhưng không giỏi môn sử (r = 0.34). Hệ số tương quan thấp phản ảnh một phần cấu trúc đề thi có vấn đề.
Cũng cần nói thêm rằng trong các kì thi PISA, hệ số tương quan giữa các môn toán và khoa học là rất cao (khoảng 0.8 đến 0.9), chứng tỏ đề thi họ soạn có hệ thống và phản ảnh trình độ học sinh.

Hình 4: Hệ số tương quan (đo lường mức độ tương quan) giữa các môn học cho Hà Giang. Số liệu được tính trên 3203 thí sinh.

Thí sinh nào có điểm 'bất thường'?

Để trả lời câu hỏi này, chúng ta có thể áp dụng khái niệm "outlier" (giá trị ngoại vi). Cách nhận dạng và xác định giá trị ngoại vi -- tức thí sinh có điểm cao hay thấp bất bình thường -- chúng ta có thể dùng hai phương pháp: phân tích đơn biến và phân tích đa biến. Tôi nghĩ phân tích đa biến thích hợp hơn, vì nó cho phép chúng ta đánh giá toàn diện các môn học. Một chỉ số quan trọng trong phân tích đa biến để nhận dạng giá trị ngoại vi là Cook's distance -- khoảng cách Cook. Tôi thử áp dụng phương pháp này cho tỉnh Hà Giang thì thấy kết quả như sau (Hình 5).

Hình 5: Biểu đồ Cook, nhận dạng các thí sinh Hà Giang có điểm "ngoại vi". Các em (19 hay 20 em) có điểm trên màu đỏ (thể hiện 4 độ lệch chuẩn từ trung bình) có thể xem là "điểm ngoại vi" (môn toán). Chú ý một em có điểm rất khác xa so với các em khác.

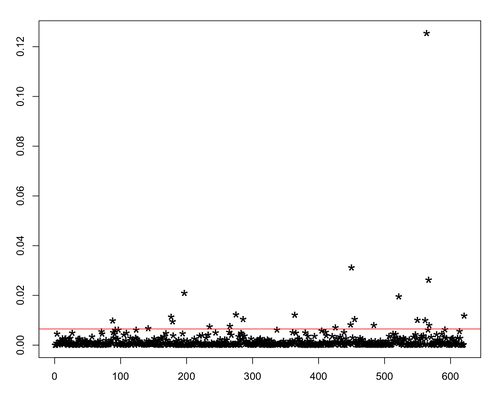
R codes:
m = lm(Math ~ Viet + English + Physics + Chemistry + Biology, data=hg)
dist = cooks.distance(m)
plot(dist, pch="*", cex=2)
abline(h = 4*mean(dist, na.rm=T), col="red")

Rõ ràng, có một số thí sinh (khoảng 20 em, trên đường màu đỏ) có thể xem là bất bình thường. Đặc biệt, có một thí sinh "ngồi" riêng một vị trí rất xa với các bạn khác. Có thể nhận dạng ID các thí sinh này dễ dàng, nhưng chắc không cần thiết.

Nói tóm lại, những dữ liệu thực tế trên đây cho thấy phân bố điểm môn toán của thí sinh tỉnh Hà Giang rất khác biệt so với 'qui luật' chung toàn quốc. Sự khác biệt này không phải là ngẫu nhiên, bởi vì trị số P quá thấp (1 trên 100 triệu). Rất có thể sự khác biệt đó là do sự can thiệp của con người.

Mời bạn đón đọc các bài viết tiếp theo bằng cách đăng kí nhận tin bài viết qua email hoặc like fanpage Thuvienkhoahoc.com để nhận được thông báo khi có cập nhật mới.

Nguồn

• Trang cá nhân của GS Tuấn