Thành viên:Nguyenthephuc/Note: Phương trình, bất phương trình vô tỉ
Thời gian/Số tiết: 120 phút/01
Bài này chúng ta xét một số phương trình, bất phương trình có chứa ẩn trong dấu căn thức bậc hai. Để giải các phương trình, bất phương trình loại này, thường ta phải khử được dấu căn thức, có nhiều phương pháp để khử căn thức. Sau đây ta làm quen với 2 phương pháp thường dùng để khử dấu căn thức: phương pháp biến đổi tương đương và đặt ẩn phụ.
Mục lục
1) Phương pháp biến đổi tương đương[sửa]
Các phép biến đổi tương đương thường dùng
-
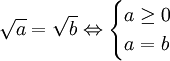 (Không
cần
điều
kiện
b
≥
0)
(Không
cần
điều
kiện
b
≥
0) -
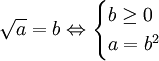 (Không
cần
điều
kiện
a
≥
0)
(Không
cần
điều
kiện
a
≥
0) -
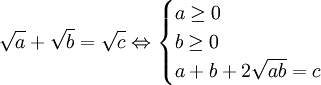 (Không
cần
điều
kiện
c
≥
0)
(Không
cần
điều
kiện
c
≥
0) -
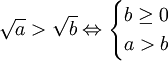
-
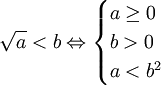
-
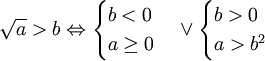
Giải các phương trình sau:
a)
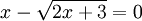
b)
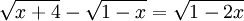
Giải các bất phương trình sau:
a)
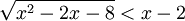
b)
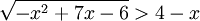
Bình luận: Nói chung, chúng ta ít gặp các bất phương trình có thể áp dụng được luôn các phép biến đổi trên, mà thường phải qua vài lần biến đổi rồi mới áp dụng được các phép biến đổi tương đương trên.
c)
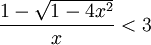
2) Phương pháp đặt ẩn phụ[sửa]
Một số phương trình, bất phương trình có thể giải dễ dàng hơn bằng cách đặt ẩn phụ
Giải
phương
trình:
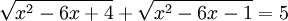
Giải
bất
phương
trình:
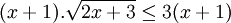
Tìm
m
để
phương
trình
sau
có
4
nghiệm
phân
biệt:
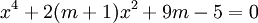
Tài liệu tham khảo[sửa]
Xem thêm[sửa]
Các ghi chú của cùng tác giả
- So sánh điểm kì thi tốt nghiệp trung học của Hà Giang và cả nước
- Học làm cha, làm mẹ
- Đọc sách 2 giờ mỗi ngày (Từ 4-6h sáng)
- Rễ, thân cành, và lá
- Sự trở lại của các thành bang
- Việt Nam học được gì từ bài học Phần Lan trong đổi mới giáo dục
- Đằng sau sự thành công của giáo dục Phần Lan là gì?
- Bí mật trong tuyển chọn và đào tạo giáo viên Phần Lan
- Chiến tranh và khó khăn - lý do khiến giáo dục Việt Nam khó phát triển
- Năng lực và các khái niệm liên quan


