Chủ đề nóng: Phương pháp kỷ luật tích cực - Cổ học tinh hoa - Những thói hư tật xấu của người Việt - Công lý: Việc đúng nên làm - Giáo án Điện tử - Sách giáo khoa - Học tiếng Anh - Bài giảng trực tuyến - Món ăn bài thuốc - Chăm sóc bà bầu - Môi trường - Tiết kiệm điện - Nhi khoa - Ung thư - Tác hại của thuốc lá - Các kỹ thuật dạy học tích cực
- Dạy học phát triển năng lực - Chương trình giáo dục phổ thông
Thành viên:Nguyenthephuc/Note: Phương trình đường tròn
Từ VLOS
Những
phương
trình
như
thế
nào
thì
được
gọi
là
phương
trình
đường
tròn?
- Số tiết 01
1) Phương trình đường tròn[sửa]
- Bài toán
Cho đường tròn (C) tâm I(a; b) và bán kính R. Điểm M có hoành độ, tung độ thỏa mãn điều kiện gì để M thuộc (C)?
- Định nghĩa
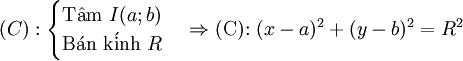 |
|
- Ví dụ
Viết phương trình đường tròn (C) biết:
- a) Tâm I(2; 1) và R = 2
- b) Tâm là gốc tọa độ và (C) qua điểm A(3; 4)
- c) (C) có đường kính AB với A(1; 1), B(3; 5)
- Định lí
|
-
Phương
trình
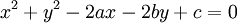 là
phương
trình
đường
tròn
nếu
là
phương
trình
đường
tròn
nếu
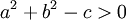
- Đường tròn 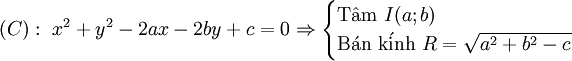
|
|
- Ví dụ
Trong các phương trình sau, phương trình nào là phương trình của một đường tròn, khi đó tìm tâm và bán kính?
-
a)
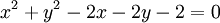
-
b)
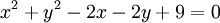
-
c)
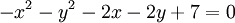
-
d)
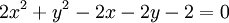
2) Phương trình tiếp tuyến tại tiếp điểm[sửa]
- Bài toán
Cho
đường
tròn
(C)
tâm
I(a;
b)
và
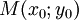
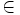 (C).
Viết
phương
trình
tiếp
tuyến
Δ
của
(C)
tại
M.
(C).
Viết
phương
trình
tiếp
tuyến
Δ
của
(C)
tại
M.
- Định lí
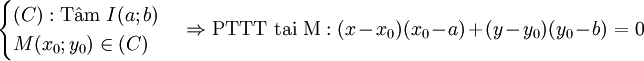 |
|
- Ví dụ
Cho
đường
tròn
(C):
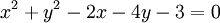 và
M(3;
4)
thuộc
đường
tròn
(C).
Viết
phương
trình
tiếp
tuyến
của
(C)
tại
M.
và
M(3;
4)
thuộc
đường
tròn
(C).
Viết
phương
trình
tiếp
tuyến
của
(C)
tại
M.
3) Bài tập về nhà[sửa]
Làm bài tập 1, 2, 3 và 6 SGK trang 83-84
Xem thêm[sửa]
Tài liệu tham khảo[sửa]
- Sách Hình học 10, NXB Giáo dục 2006
- Sách Hình học Nâng cao 10, NXB Giáo dục 2006
Các ghi chú của cùng tác giả
- So sánh điểm kì thi tốt nghiệp trung học của Hà Giang và cả nước
- Học làm cha, làm mẹ
- Đọc sách 2 giờ mỗi ngày (Từ 4-6h sáng)
- Rễ, thân cành, và lá
- Sự trở lại của các thành bang
- Việt Nam học được gì từ bài học Phần Lan trong đổi mới giáo dục
- Đằng sau sự thành công của giáo dục Phần Lan là gì?
- Bí mật trong tuyển chọn và đào tạo giáo viên Phần Lan
- Chiến tranh và khó khăn - lý do khiến giáo dục Việt Nam khó phát triển
- Năng lực và các khái niệm liên quan


