Thành viên:Nguyenthephuc/Note: Wiki hóa

Thừa Thiên Huế

• Một số giáo án điện tử chọn lọc bậc học THPT, THCS & Tiểu học Năm học 2006 của Sở GD & ĐT Thừa Thiên Huế

Đại học sư phạm TP Hồ Chí Minh, Khoa công nghệ

Những tư liệu dưới đây đã được Nguyễn Thanh Vinh - tác giả website: http://khcn-sdh.hcmup.edu.vn/tmp/giaoan/ đồng ý đăng tải trên VLOS và phát hành chúng dưới phạm vi công cộng.

---

MỘT SỐ GIÁO ÁN, BÀI GIẢNG

Các giáo án, bài giảng sưu tập ở đây không phải là mẫu mực để bạn tuân theo. Hầu hết các giáo án đã được xin phép tác giả và được phép phân phối lại.

Cảm ơn các tác giả đã đóng góp, hỗ trợ tài liệu.

1. Các khái niệm mở đầu về hình không gian. Tăng Minh Dũng soạn bằng LaTeX (File PDF) và GeospaceW, PowerPoint.

2. Phép chiếu song song và hình biểu diễn của một hình không gian, MS. PowerPoint.

3. Bài tập về quĩ tích trong không gian. Tăng Minh Dũng soạn bằng LaTeX (trình diễn), GeospaceW. Học cách soạn giáo án LaTeX qua Định lí cosin (source), Bài tập Định lí đảo tam thức bậc 2 (source).

4. Toàn bộ giáo án Tin học khối 10, 11, 12 (Word). Các bài thực tập của sinh viên Tin học (2006).

5. Toàn bộ giáo án Toán học khối 10, 11, 12 (Word, 2 bộ). Một số giáo án soạn theo sách mới 2006 (Đại số 10, Hình học 10)

Lớp 10

STT	Môn - Chương	Nội dung	Đề cương - kiểm tra
1		Kiểm tra chất lượng đầu năm lớp 10
2	Đại số 10 - Chương 1	Tập hợp - mệnh đề	kt_daiso10_c1
3	Đại số 10 - Chương 2	Hàm số	kt_daiso10_c2, kt_daiso10_c2_2
4	Đại số 10 - Chương 3	Phương trình và bất phương trình bậc nhất
5	Đại số 10 - Chương 4	Phương trình và bất phương trình bậc hai
6	Đại số 10 - Chương 5	Sai số
8	Hình học 10 - Chương 1	Vectơ	kt_hinhhoc10_c1
9	Hình học 10 - Chương 2	Hệ thức lượng trong tam giác và trong đường tròn	de cuong on tap HKI - Lop 10
10	Hình học 10 - Chương 3	Phép biến hình (Phép dời hình và phép đồng dạng)	decuong-lop 10 - hoc ki 2

Lớp 11

STT	Môn - Chương	Nội dung	Đề cương, kiểm tra
1	Giải tích 11 - Chương 1	Hàm số lượng giác	kt_giaitich11_45_1, dektraGT11.CI
2	Giải tích 11 - Chương 2	Phương trình và hệ phương trình lượng giác	kt_giaitich11_c2_45, PTLG 1 ban sao chep, kt_giaitich11_CII, kt_giaitich11_cII(pt-hptlg)
3	Giải tích 11 - Chương 3	Dãy số - cấp số cộng - cấp số nhân	Đề cương ôn tập hkI-11, Đề thi hkI(04-05) + Đáp án , dethiHKI.NH(05-06)
4	Giải tích 11 - Chương 4	Giới hạn	kt_giaitich11_c4_45
5	Giải tích 11 - Chương 5	Hàm số mũ
6	Giải tích 11 - Chương 6	Hàm số logarit
7	Hình học 11 - Chương 1	Đại cương về đường thẳng và mặt phẳng	kt_hinhhoc11_45
8	Hình học 11 - Chương 2	Quan hệ song song	kt_hinhhoc11_45_2 (có đáp án)
9	Hình học 11 - Chương 3	Quan hệ vuông góc
10	Hình học 11 - Chương 4	Mặt cầu và mặt tròn xoay	kt_hinhhoc11_c4
11	Hình học 11 - Chương 5	Diện tích - Thể tích	decuong HKII-lop 11, dethihkII-K11 Đề thi học kì 2 và đề kiểm tra chương 5

Lớp 12

STT	Môn - Chương	Nội dung	Đề cương - Kiểm tra
1	?	?	?
2	?	?	?

Nguồn

• http://khcn-sdh.hcmup.edu.vn/tmp/giaoan/

Pham Loi Vu 2005

The Dirichlet initial-boundary-value problems for sine and sinh-Gordon equations on a half-line

Pham Loi Vu 2005 Inverse Problems 21 1225-1248 doi:10.1088/0266-5611/21/4/003

Pham Loi Vu

Institute of Mechanics, Vietnamese Academy of Science and Technology, 264 Doi Can Street, Hanoi, Vietnam

Abstract. The paper deals with the problems for the sine-Gordon and sinh-Gordon equations on a half-line:

$v_{{xt}}={\mbox{sin}}\,v,\qquad \ 0\leq x<\infty ,\quad 0\leq t\leq T$

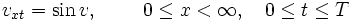(1)

$v_{{xt}}={\mbox{sh}}\,v,\qquad \ \ 0\leq x<\infty ,\quad 0\leq t\leq T$

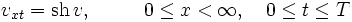(2)

with the given initial and boundary conditions:

$v(x,0)=v(x),\qquad v_{x}(x)\ {\mbox{is a real rapidly decreasing function}}$

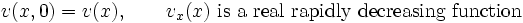(3)

$v(0,t)=h(t),\qquad h(t)\ {\mbox{is a continuous real-valued function}}$

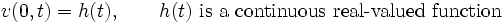(4)

The Dirichlet initial-boundary-value problem (IBVP) (1), (3), (4) is associated with the scattering problem (SP) for the system

$u_{x}=U_{1}u,\quad U_{1}={{\rm {i}}}\lambda J+{\frac {{\rm {i}}}{2}}{\begin{pmatrix}0&v_{x}\\v_{x}&0\end{pmatrix}},\!\!\qquad 0\leq x<\infty ,\quad 0\leq t\leq T$

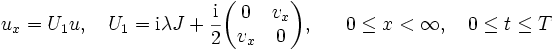(5)

J = diag(1, - 1), u = (u₁, u₂), with the boundary condition:

$u_{1}(0,\lambda )=u_{2}(0,\lambda ).\,$

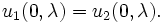(6)

The Dirichlet IBVP (2)–(4) is associated with the SP for the system:

$u_{x}=U_{2}u,\quad U_{2}={{\rm {i}}}\lambda J+{\frac {{\rm {i}}}{2}}{\begin{pmatrix}0&v_{x}\\-v_{x}&0\end{pmatrix}},\qquad 0\leq x<\infty ,\quad 0\leq t\leq T$

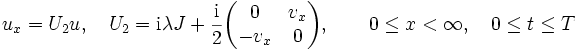(7)

with the boundary condition (6).

We apply a formalism of the direct and inverse SP (5), (6) ((7), (6)) to investigate the considered IBVPs. The difficulty associated with these problems is that the time dependence of the scattering data set s of the SP is determined by unknown boundary values (BVs) at x = 0 of the Jost solutions of (5) ((7)) and more, the evolution equations for BVs contain unknown boundary data (BD). We overcome this difficulty in the following way. We show that the evolution of the BD is described by a linear Volterra integral equation, the solution of which is found in terms of the given (3) and (4). Then the BVs are calculated in terms of (3) and (4). We find the necessary and sufficient conditions on the quantities of the data set s which ensure a unique solution of the inverse problem. Therefore, the antiderivative of the recovered potential is the solution of the considered IBVP.

Print publication: Issue 4 (August 2005)

Received 8 December 2004

Published 19 May 2005

Nguồn

• http://www.iop.org/EJ/abstract/-search=16647119.1/0266-5611/21/4/003

Liên kết đến đây

• Thành viên:Nguyenthephuc/Wiki hóa