Danh mục và lịch sử các đường cong/Phần 1. Từ As đến Co (1 – 10)
Mục lục
- 1 1. Astroid
- 2 2. Bicorn (đường mào gà)
- 3 3. Cardioid (đường hình tim)
- 4 4. Cartesian Oval (đường oval Descartes)
- 5 5. Cassinian Ovals (đường oval Cassini)
- 6 6. Catenary (đường dây xích)
- 7 7. Cayley's sextic (đường bậc 6 Cayley)
- 8 8. Circle (đường tròn)
- 9 9. Cissoid of Diocles (đường cissoid Diocles)
- 10 10. Cochleoid (đường ốc sên Cochleoid)
- 11 Tham khảo
- 12 Bản quyền
- 13 Mục lục
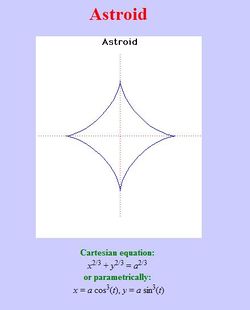
1. Astroid[sửa]
Phương trình đường cong trong hệ tọa độ Descartes:
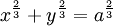
Phương trình đường cong dạng tham số:
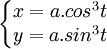
Astroid lần đầu tiên được Johann Bernoulli đề cập đến vào khoảng 1691-1692. Nó cũng xuất hiện trong các công trình của Leibniz của năm 1715. Đôi khi được gọi là tetracuspid vì lý do nó có 4 chỏm.
Astroid chỉ chính thức có tên gọi vào năm 1836 trong một cuốn sách xuất bản ở Vienna. Astroid được biết đến dưới các tên gọi khác nhau bao gồm cả cubocycloid và paracycle vào sau năm 1836.
Chu
vi
của
astroid
là
6a
và
diện
tích
của
nó
là
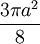
Gradient
của
tiếp
tuyến
(T)
từ
một
điểm
với
tham
số
p
là: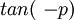 .
Phương
trình
tiếp
tuyến
(T):
.
Phương
trình
tiếp
tuyến
(T):
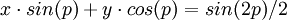
(T)
cắt
trục
Ox
và
Oy
tại
X
và
Y
tương
ứng
thỏa
mãn
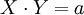 .
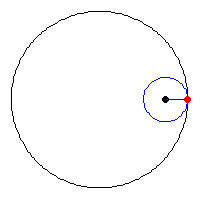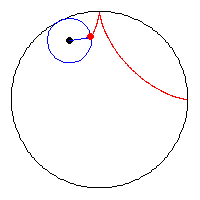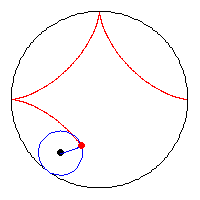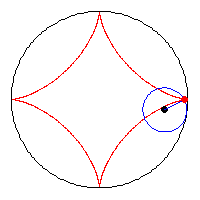
Astroid
được
hình
thành
bằng
cách
lăn
một
vòng
tròn
bán
kính
a
/
4
bên
trong
một
vòng
tròn
có
bán
kính
a.
.
Astroid
được
hình
thành
bằng
cách
lăn
một
vòng
tròn
bán
kính
a
/
4
bên
trong
một
vòng
tròn
có
bán
kính
a.
Astroid là điểm tụ quang của hình delta với tia song song theo hướng bất kỳ.
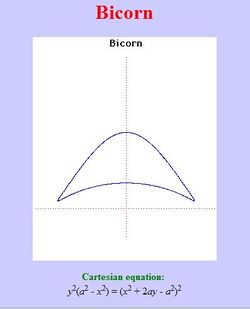
2. Bicorn (đường mào gà)[sửa]
Phương trình đường cong trong hệ tọa độ Descartes:
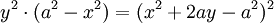
Bicorn (còn gọi là đường mào gà) là tên của một tập hợp các đường cong bậc 4 (quartic) nghiên cứu của Sylvester năm 1864. Các đường cong tương tự đã được Cayley nghiên cứu vào năm 1867. Các bicorn đặc biệt khác được Sylvester và Cayley đưa ra từ phương trình bậc 4 (quartic) khác nhau, nhưng dạng phương trình và đồ thị trên đây có dạng đơn giản hơn và chủ yếu là đồng dạng về đồ thị.
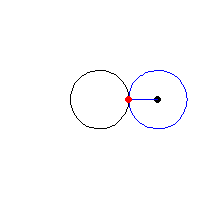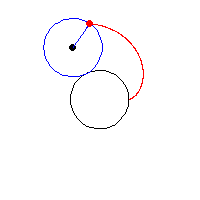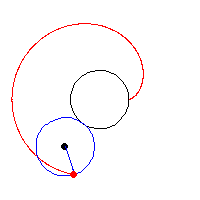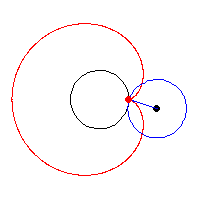
3. Cardioid (đường hình tim)[sửa]
Phương trình đường cong trong hệ tọa độ Descartes
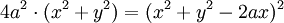
Phương trình đường cong trong tọa độ cực:
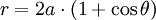
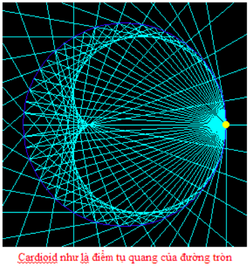
Cardioid là tên gọi đầu tiên của một đường cong được de Castillon viết trong một bài báo đăng ở tuyển tập Philosophical Transactions of the Royal Society 1741. Đó là quỹ tích của một điểm trên chu vi của đường tròn lăn không trượt trên chu vi của một đường tròn khác có cùng bán kính. Tên của phương trình này còn có nghĩa là "hình trái tim”. Năm 1708 La Hire đã tìm ra công thức tính chu vi của nó, và do đó ông tuyên bố là người đầu tiên phát hiện ra các đường cong Cardioid. Theo công thức nêu trên chu vi của nó là 16a. Cardioid thật ra là một trường hợp đặc biệt của đường cong Limacon
Pascal (Etienne Pascal) và như vậy, nếu nói một cách hợp lý, những nghiên cứu về đường cong này đã có từ rất lâu trước khi Castillon La Hire công bố. Với bất kỳ gradient nào cho trước trên cardioid luôn luôn có chính xác ba tiếp tuyến song song với nhau.
Chiều
dài
của
bất
kỳ
dây
nhau
thông
qua
các
điểm
đỉnh
là
4a
và
diện
tích
của
cardioid
là
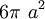 .
Phương
trình
tham
số
trong
hệ
tọa
độ
Descartes
cho
cardioid,
cụ
thể
là
.
Phương
trình
tham
số
trong
hệ
tọa
độ
Descartes
cho
cardioid,
cụ
thể
là
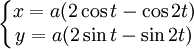
Có một số đường cong khác, hình trái tim được do Kurt Eisemann (San Diego State University, USA) cung cấp:
Phương trình đường cong trong hệ tọa độ Descartes:
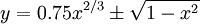
Phương trình đường cong trong hệ tọa độ cực:
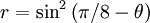
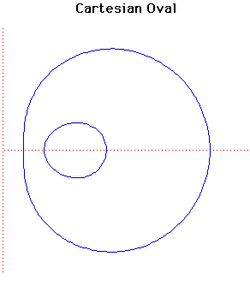
4. Cartesian Oval (đường oval Descartes)[sửa]
Phương trình đường cong trong hệ tọa độ Descartes:
![[(1-m^{2}).(x^{2}+y^{2})+2m^{2}cx+a^{2}-m^{2}c^{2}]^{2}=4a^{2}\cdot (x^{2}+y^{2})](https://tusach.thuvienkhoahoc.com/images/math/d/6/7/d67b8245315a166ed440e5131606c21e.png)
Đường
cong
này
bao
gồm
2
đường
oval
lồng
nhau,
là
quỹ
tích
của
một
điểm
P
có
khoảng
cách
là
s
và
t
từ
hai
điểm
cố
định
S
và
T
thỏa
mãn:
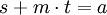 .
Khi
c
là
khoảng
cách
giữa
S
và
T
phương
trình
đường
cong
có
thể
được
biểu
diễn
như
trên.
.
Khi
c
là
khoảng
cách
giữa
S
và
T
phương
trình
đường
cong
có
thể
được
biểu
diễn
như
trên.
Các đường cong này lần đầu tiên được Descartes nghiên cứu vào năm 1637 và đôi khi được gọi là "Hình bầu dục Descartes ".Đường cong cũng được nghiên cứu bởi Newton khi phân loại các đường cong bậc 3 (cubic).
Oval
Cartesian
có
phương
trình
lưỡng
cực:
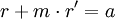 .
Nếu
.
Nếu
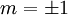 thì
Oval
Descartes
(C)
là
một
hình
nón
trung
tâm
Nếu
thì
Oval
Descartes
(C)
là
một
hình
nón
trung
tâm
Nếu
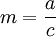 thì
đường
cong
là
dạng
đặc
biệt
thuộc
họ
Limacon
Pascal
(Étienne
Pascal).
Trong
trường
hợp
này,
hình
bầu
dục
bên
trong
tiếp
xúc
với
bên
ngoài.
Hình
bầu
dục
Cartesian
là
những
đường
cong
anallagmatic.
thì
đường
cong
là
dạng
đặc
biệt
thuộc
họ
Limacon
Pascal
(Étienne
Pascal).
Trong
trường
hợp
này,
hình
bầu
dục
bên
trong
tiếp
xúc
với
bên
ngoài.
Hình
bầu
dục
Cartesian
là
những
đường
cong
anallagmatic.
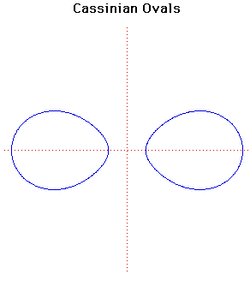
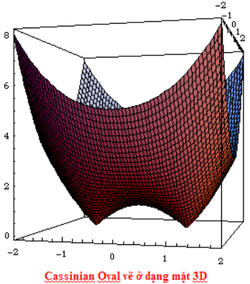
5. Cassinian Ovals (đường oval Cassini)[sửa]
Phương trình đường cong trong hệ tọa độ Descartes:
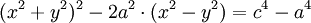
Các
hình
bầu
dục
Cassinian
là
quỹ
tích
của
một
điểm
P
di
chuyển
sao
cho
tích
của
2
khoảng
cách
từ
P
đến
hai
điểm
cố
định
S
và
T
[
trong
trường
hợp
này
điểm
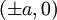 ]
là
một
hằng
số.
Hình
dạng
của
đường
cong
phụ
thuộc
vào
tỷ
số
c
/
a
]
là
một
hằng
số.
Hình
dạng
của
đường
cong
phụ
thuộc
vào
tỷ
số
c
/
a
- Nếu c > a thì đường cong bao gồm hai vòng.
- Nếu c < a đường cong bao gồm một vòng đơn.
- Nếu c = a đường cong có dạng Lemniscate Bernoulli (là một trong tám đường cong kiểu mẫu giới thiệu bởi Jacob Bernoulli).
Cassinian ovals lần đầu tiên được Giovanni Cassini khảo sát vào năm 1680 khi ông đang nghiên cứu các chuyển động tương đối của Trái đất và Mặt trời. Cassini tin rằng mặt trời đi vòng quanh trái đất trên một trong các hình bầu dục, với Trái đất tại một tiêu điểm của hình bầu dục đó. Cassini đã giới thiệu các đường cong của mình 14 năm trước khi Jacob Bernoulli mô tả các lemniscate của mình.
Hình
bầu
dục
Cassinian
là
đường
cong
anallagmatic.
Họ
đường
cong
này
được
xác
định
bởi
phương
trình
lưỡng
cực:
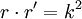
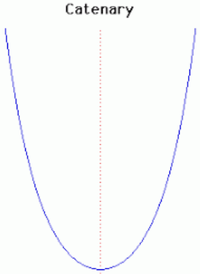
6. Catenary (đường dây xích)[sửa]
Phương trình đường cong trong hệ tọa độ Descartes:
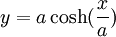
Dây xích có hình dạng hoàn hảo của một chuỗi, cố định ở 2 đầu và chịu tác động bởi lực hấp dẫn. Phương trình của nó do Leibniz, Huygens và Johann Bernoulli đưa ra năm 1691, nhằm giải quyết các thách thức của vấn đề đặt ra bởi Jacob Bernoulli với mục đích là đi tìm phương trình của chuỗi đường cong.
Huygens là người đầu tiên sử dụng tên gọi dây xích trong một bức thư cho Leibniz năm 1690 và David Gregory đã trình bày lý thuyết về dây xích vào năm 1690. Năm 1669 Jungius đã bác bỏ ý tưởng của Galileo cho rằng đường cong của một chuỗi treo dưới tác dụng lực hấp dẫn sẽ là một parabol.
Dây xích là quỹ tích của tiêu điểm thuộc một parabol lăn không trượt dọc theo một đường thẳng.
Năm 1744 Euler chỉ ra rằng, một dây xích khi quay quanh tiệm cận của nó sẽ tạo ra mặt cực tiểu duy nhất.
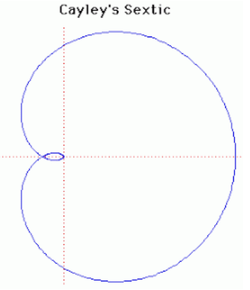
7. Cayley's sextic (đường bậc 6 Cayley)[sửa]
Phương trình đường cong trong hệ tọa độ Descartes:
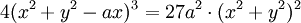
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
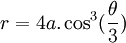
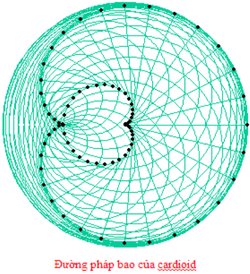
Đường cong này do Maclaurin phát hiện đầu tiên, nhưng công trình nghiên cứu chi tiết thuộc về Cayley. Cayley's sextic do RC Archibald đặt tên để phân loại các đường cong trong một bài báo xuất bản ở Strasbourg vào năm 1900. Đường pháp bao của Sextic Cayley là một đường cong nephroid
8. Circle (đường tròn)[sửa]
Phương trình đường cong trong hệ tọa độ Descartes:
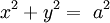
Phương trình đường cong tham số:
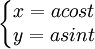
Phương trình đường cong trong hệ tọa độ cực:
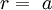
Các nghiên cứu về đường tròn được lịch sử ghi lại từ rất lâu. Việc phát minh ra bánh xe là một phát hiện cơ bản và có giá trị nhất về đường tròn. Người Hy Lạp vẫn xem người Ai Cập như là những người tiên phong phát minh về hình học. Ahmes tác giả của bản văn papyrus Rhind, đã đưa ra một quy tắc để xác định diện tích của một vòng tròn tương ứng với số π = 256/81 hoặc khoảng 3,16.
Các định lý đầu tiên liên quan đến vòng tròn do Thales khoảng năm 650 trước Công nguyên. Sách III về các yếu tố của hình học Euclid đã đề cập đến tínhchất của đường tròn và các bài toán liên quan đến đa giác.
Một trong những bài toán cổ Hy Lạp là tìm kiếm một hình vuông có diện tích bằng với một đường tròn cho trước và Anaxagoras (450 BC) được ghi nhận là nhà toán học đầu tiên nghiên cứu vấn đề này.
Diện
tích
của
đường
tròn
là
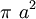 và
chu
vi
là
và
chu
vi
là
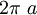
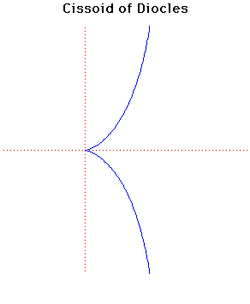
9. Cissoid of Diocles (đường cissoid Diocles)[sửa]
Phương trình đường cong trong hệ tọa độ Descartes:
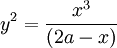
Phương trình đường cong trong hệ tọa độ cực:
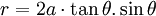
Đường
cong
này
(có
nghĩa
là
"
hình
ivy
")
được
Diocles
phát
hiện
khoảng
180
trước
Công
nguyên
khi
ông
giải
quyết
bài
toán
nhân
đôi
một
khối
lập
phương
bằng
phương
pháp
hình
học.
Tên
gọi
đầu
tiên
của
nó
xuất
hiện
trong
công
trình
của
Geminus
khoảng
100
năm
sau,
Fermat
và
Roberval
giải
quyết
bài
toán
tiếp
tuyến
vào
năm
1634.
Đến
năm
1658,
Huygens
và
Wallis
tìm
thấy
diện
tích
giới
hạn
bởi
đường
cong
và
tiệm
cận
của
nó
là
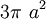 .
Từ
một
điểm
bất
kỳ
cho
trước
có
thể
có
một
hoặc
ba
tiếp
tuyến
với
các
cissoid.
.
Từ
một
điểm
bất
kỳ
cho
trước
có
thể
có
một
hoặc
ba
tiếp
tuyến
với
các
cissoid.
Cissoid của Diocles là đường quay của đỉnh của một parabol trên một parabol bằng với chính nó. Newton đã đưa ra một phương pháp vẽ các Cissoid Diocles bằng cách sử dụng hai đoạn thẳng vuông góc bằng nhau. Nếu di chuyển cặp đoạn thẳng này sao cho một đoạn luôn luôn đi qua một điểm cố định và điểm cuối của đoạn kia trượt dọc theo một đường thẳng thì quỹ tích trung điểm của đoạn thẳng trượt này tạo ra Cissoid Diocles.
Diocles là nhân vật cùng thời với Nicomedes. Ông đã nghiên cứu cissoid trong khi giải quyết bài toán tìm cạnh của một khối lập phương có thể tích gấp đôi của một khối lập phương cho trước. Ông cũng nghiên cứu các vấn đề của Archimedes khi cắt một hình cầu bằng một mặt phẳng thành hai phần theo một tỷ lệ nhất định. Trong bài bình luận về công trình của Archimedes về hình cầu và hình trụ, khái niệm vê cissoid xuất hiện và được cho là của Diocles đề xuất.
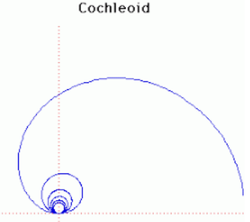
10. Cochleoid (đường ốc sên Cochleoid)[sửa]
Phương trình đường cong trong hệ tọa độ cực:
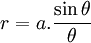
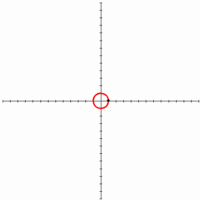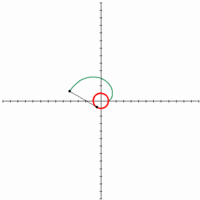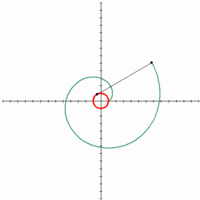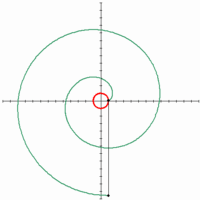
Cochleoid có nguồn gốc vào năm 1884 do các tác giả Benthan và Falkenburg đề xuất có nghĩa là đường cong hình ốc sên. J Peck đã thảo luận các vấn đề về đường cong này vào năm 1700. Các hình dạng đưa ra ở đây là do một người Bỉ tên Joseph Neuberg.
Tham khảo[sửa]
1. http://www-history.mcs.st-andrews.ac.uk/Curves/Curves.html
2. http://www-history.mcs.st-andrews.ac.uk/
3. Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers. Department of Mathematics, Computer Science, and Statistics,Bloomsburg University Bloomsburg, Pennsylvania 17815.
4. A Handbook on curves and their properties. Robert C. Yates, printed by Edwards Brothers, Inc - Ann Arbor, Michigan U.S.A.
Bản quyền[sửa]
Biên tập và trích dịch.
Ngày 01/04/2012
Mục lục[sửa]
- Giới thiệu
- Phần 1. Từ As đến Co (1 – 10)
- Phần 2. Từ Co đến Eq (11 – 21)
- Phần 3. Từ Fe đến Ka (22 – 32)
- Phần 4. Từ Ka đến Pa (33 – 42)
- Phần 5. Từ Pe đến Rh (43 – 48)
- Phần 6. Từ Ri đến Sp (49 – 53)
- Phần 7. Từ Sp đến Tr (54 – 58)
- Phần 8. Từ Tr đến Wi (59 – 63)
Bài liên quan
Liên kết đến đây
- Danh mục và lịch sử các đường cong
- Bản mẫu:Danh mục và lịch sử các đường cong
- Danh mục và lịch sử các đường cong/Phần 2. Từ Co đến Eq (11 – 21)
- Danh mục và lịch sử các đường cong/Phần 3. Từ Fe đến Ka (22 – 32)
- Danh mục và lịch sử các đường cong/Phần 4. Từ Ka đến Pa (33 – 42)
- Danh mục và lịch sử các đường cong/Phần 5. Từ Pe đến Rh (43 – 48)
- Danh mục và lịch sử các đường cong/Phần 6. Từ Ri đến Sp (49 – 53)
- Danh mục và lịch sử các đường cong/Phần 7. Từ Sp đến Tr (54 – 58)
- Danh mục và lịch sử các đường cong/Phần 8. Từ Tr đến Wi (59 – 63)