Danh mục và lịch sử các đường cong/Phần 7. Từ Sp đến Tr (54 – 58)

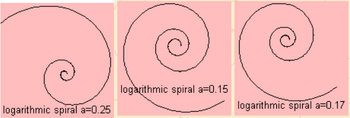
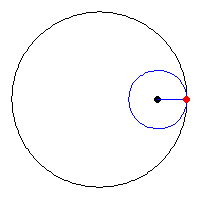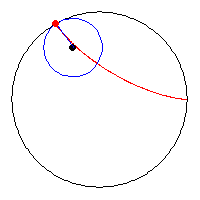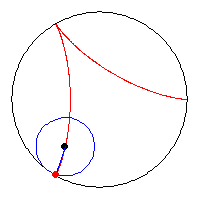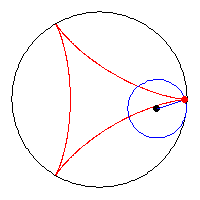
54. Spiral Logarithm (Đường xoắn ốc logarith)

Phương trình đường cong trong hệ tọa độ cực: $r=e^{{a\theta }}\,$

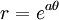
Đây là đường xoắn ốc có bán kính r tăng theo hàm mũ với đối số góc 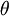$\theta$ . Mối quan hệ logarit giữa bán kính và góc dẫn đến tên của nó là đường xoắn ốc logarit hoặc logistique (theo tiếng Pháp).

Khoảng cách của bán kính tính từ gốc O đến các điểm thuộc đường cong là theo cấp số nhân.

Đường cong này còn được gọi là đường xoắn ốc Bernoulli - vốn là sở thích của Jakob (I) Bernoulli (1654-1705). Theo yêu cầu của ông, bia mộ trong nhà thờ Munster ở Basel, được trang trí bằng một hình xoắn ốc logarit.

Nó cũng mang một tên gọi khác là đường xoắn ốc Fibonacci. Về hình thức đường cong này trông giống như đường xoắn ốc Archimedes, người ta tìm thấy có văn bản Latinh đính kèm như sau: eadem mutata resurgo - có nghĩa là: " dù có đổi thay, vẫn như là một . Điều này cũng đề cập đến việc cho dù có các tính toán khác nhau nhưng các đường cong vẫn nguyên vẹn.

Tuy nhiên, Rene Descartes (1638)mới là người đầu tiên nghiên cứu các đường cong xoắn ốc. Torricelli cũng góp phần nghiên cứu một cách độc lập, và từ đó ông tìm thấy chiều dài của đường cong.

Chúng ta thường thấy đường cong xoắn ốc logarith trong tự nhiên, đối với các tổ chức có sự tăng trưởng tỷ lệ với kích thước của chúng. Một ví dụ là vỏ sò Nautilus, nơi có một loại bạch tuộc ký sinh.

Vì tính tỷ lệ tương xứng như vậy nên các đường cong thường có tên gọi là đường xoắn ốc tăng trưởng.

D'Arcy Thompson giải thích đường cong trong cuốn sách của ông có tựa đề " Tăng trưởng và hình thái ".

Hai tính chất vật lý cũng liên quan đến xoắn ốc là:

- Lực làm cho một chất điểm chuyển động trên một quỹ đạo xoắn ốc logarit tỷ lệ thuận với ${\frac {1}{r^{3}}}$

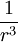
- Một hạt tích điện chuyển động trong một từ trường đều, vuông góc với trường đó, tạo thành một đường xoắn ốc logarit.

Johan Gielis, một nhà thực vật học Bỉ đã mở rộng đường xoắn ốc logarit thành đường siêu xoắn ốc (super spiral).

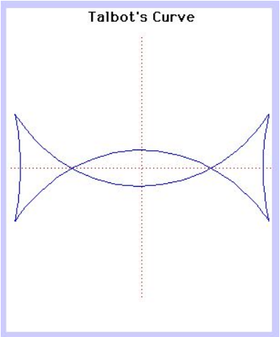
55. Talbot’s Curve (Đường cong Talbot)

Phương trình tham số trong hệ tọa độ Descartes:

${\begin{cases}x=(1+e^{2}\sin ^{2}t)a\cos t\\y=a\sin t(1-2e^{2}+e^{2}\sin ^{2}t)/{\sqrt {1-e^{2}}}\end{cases}}$

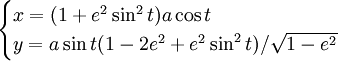
Với $e={\frac {c}{a}},c={\sqrt {a^{2}-b^{2}}}$

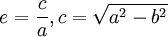
Đường cong này đã được Talbot nghiên cứu.

Henry Fox Talbot thường được biết đến hiện nay với danh tính này. Tuy nhiên, có một số tên khác ông vẫn sử dụng như Henry F Talbot hoặc H. F Talbot..

Cha của Henry là William Talbot Davenport và mẹ của ông là Elisabeth Theresa Fox-Strangways. Davenport Talbot quản lý của Tu viện Lacock ở Wiltshire nơi đã thuộc sở hữu của gia đình Talbot từ những năm 1500. Cha của ông, Davenport Talbot mất khi ông chỉ có năm tháng tuổi để lại người góa phụ trẻ Elisabeth trong một hoàn cảnh khó khăn về kinh tế. Tabot vào học trường nội trú Rottingdean khi ông được tám tuổi, chính tại đây Henry Talbot đã gặp nhà thiên văn học William Herschel.

Năm 1810, Henry đến trường trung học Harrow, nơi ông vẫn ở cho đến 1815 và sau đó chuẩn bị vào bậc đại học. Khi còn là một cậu bé, Henry Talbot đã thể hiện sự tò mò về thế giới tự nhiên, đặc biệt là trong toán học, ngôn ngữ, chính trị, thực vật học, quang học và thiên văn học.

Talbot đã được đào tạo chính quy tại Trinity College, Cambridge, năm 1817; ở đó ông đã từng giành được giải thưởng về thi ca Hy Lạp, và tốt nghiệp danh dự về bộ môn toán học năm 1821.

Sau đó Henry Talbot được bầu là Uỷ viên của Hội Thiên văn Hoàng gia mới được thành lập vào năm 1822. Trong lĩnh vực nghiên cứu toán học, ông rất cần mẫn nhưng sở thích chính là du lịch, đặc biệt rất ưa thích phong cảnh đất nước Ý.

Talbot có các bài báo về tích phân elliptic, dựa trên công trình nghiên cứu của Euler, Legendre, Jacobi và Abel. Trước khi gặp John Herschel tại Munich vào năm 1824 (con trai của nhà thiên văn học William Herschel) ông đã công bố sáu bài báo toán học, và cả hai người đều có nhiều quan điểm khoa học tương đồng, ví dụ như cả hai đều là các nhà toán học và cùng là nghiên cứu sinh Hội Thiên văn Hoàng gia. Họ nhanh chóng trở thành bạn, chẳng bao lâu sau sở thích của Talbot chuyển hướng sang nghiên cứu tính chất ánh sáng. Vào thời điểm này David Brewster, nhà vật lý Scotland, cũng đã từng tiến hành các thí nghiệm quang học và ông đã cùng với Talbot công bố một số bài báo về lĩnh vực này. Talbot đã được bầu là Uỷ viên của Hội Hoàng gia vào năm 1831 vì công trình toán học của mình. Ngoài ra Talbot cũng công bố nhiều kết quả nghiên cứu khoa học về thiên văn và vật lý.

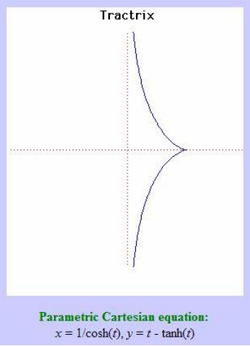
56. Tractrix (Đường cong Tractrix)

Phương trình tham số trong hệ tọa độ Descartes:

${\begin{cases}x={\frac {1}{\cosh(t)}}\\y=t-\tanh(t)\end{cases}}$

Tractrix xoay quanh tiệm cận của nó tạo thành một hình giả cầu -pseudosphere

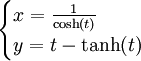
Tractrix đôi khi được gọi là một đường cong tractory hoặc đường cong đo đẳng tiếp (equitangential). Huygens lần đầu tiên nghiên cứu và đặt tên cho đường cong này vào năm 1692. Sau đó, Leibniz, Johann Bernoulli và những người khác đã tiếp tục khảo sát các tính chất đường cong.

Nghiên cứu về đường cong tractrix bắt đầu với các bài toán sau đây được Leibniz đặt ra.

Quỹ đạo của một vật được kéo dọc theo một mặt phẳng nằm ngang bởi một dây có độ dài cố định khi điểm cuối dây không nối với vật di chuyển dọc theo một đường thẳng trong mặt phẳng là gì?

Ông đã giải quyết điều này bằng cách sử dụng trục là một tiệm cận của tractrix.

Các đường pháp bao ngoài của một tractrix là một dây xích - catenary. Một trong số các thuộc tính của các tractrix là độ dài của một đoạn tiếp tuyến từ điểm tiếp xúc đến tiệm cận một là hằng số. Diện tích giới hạn bởi tractrix và tiệm cận của nó là hữu hạn.

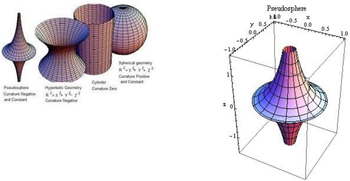
Khi tractrix xoay quanh tiệm cận của nó ta thu được kết quả là một hình giả cầu -pseudosphere. Đây là một bề mặt có độ cong âm không đổi, và đã được Beltrami năm 1868 sử dụng trong việc hiện thực hóa cụ thể các khái niệm của ông về hình học phi Euclide.

Vài nét về tác giả bài toán nghiên cứu đường cong tractrix.

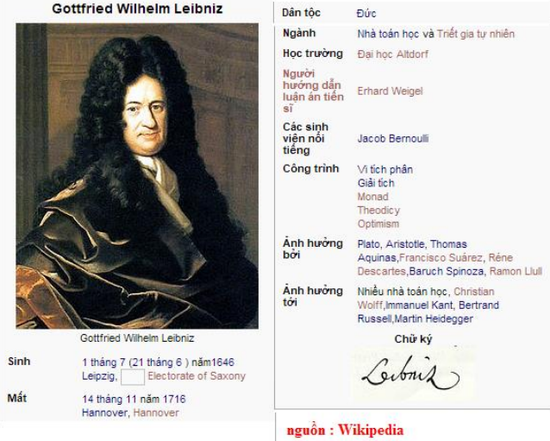
Gottfried Wilhelm Leibniz (cũng là Leibnitz hay là von Leibniz (1 tháng 7 (21 tháng 6) năm 1646 – 14 tháng 11năm 1716) là một nhà bác học người Đức có các tác phẩm bằng tiếng Latin và tiếng Pháp.

Ông từng được đào tạo về luật và triết học, đồng thời là tham vấn cho hai gia đình quý tộc lớn ở Đức. Từ đó Leibniz đã có một sự nghiệp chính trị với các vấn đề ngoại giao ở châu Âu trong thời đại của ông. Leibniz giữ vị trí quan trọng trong cả lịch sử triết học và lịch sử toán học. Ông khám phá ra vi tích phân độc lập với Isaac Newton, và sau này các kí hiệu của ông được sử dụng rộng rãi. Ông cũng khám phá ra hệ thống số nhị phân, nền tảng của hầu hết các cấu trúc máy tính hiện đại. Trong triết học, ông được nhớ đến nhiều nhất với chủ nghĩa lạc quan. Kết luận của ông về vũ trụ của nhân loại, theo một nghĩa giới hạn, là một vũ trụ tốt nhất mà Thượng Đế có thể tạo ra. Leibniz cùng với René Descartes và Baruch Spinoza, là một trong ba nhà lý luận (rationalist) nổi tiếng của thế kỉ 17. Quan điểm triết học của ông cũng có khuynh hướng quay ngược về truyền thống Scholastic, nhờ đó ông dự đoán trước về sự xuất hiện logic hiện đại và triết học phân tích. Leibniz có nhiều đóng góp lớn về vật lý và kỹ thuật, và dự đoán những khái niệm sau này nổi lên trong sinh học, y học, địa chất, lý thuyết xác suất, tâm lý học, ngôn ngữ học và công nghệ thông tin. Ông cũng viết nhiều tiểu luận về chính trị, luật học, đạo đức học, thần học, lịch sử và ngữ văn. Đóng góp của ông trong nhiều lĩnh vực khác nhau xuất hiện rải rác trong các tạp chí và với khoảng mười ngàn lá thư và những bản thảo chưa xuất bản. Nhiều bản thảo của ông được viết bằng tốc kí, sử dụng sáng chế của riêng ông khi sử dụng số nhị phân để mã hóa các chuỗi kí tự. Cho đến nay, không có sưu tập đầy đủ về những tác phẩm và bản thảo của Leibniz, và do đó không thể thống kê hết những thành tựu ông đạt được.

Tóm tắt sự nghiệp của Leibniz:

1646-1666: những năm định hình cho các hoạt động trong tương lai.

1666–74: Chủ yếu phục vụ cho Vương công-Tuyển hầu tước xứ Mainz, Johann Philippvon Schönborn, và quan Thượng thư của Phủ Lãnh chúa xứ Mainz là Nam tước von Boineburg.

1672–76. Sống ở Paris, có hai lần ghé thăm quan trọng tới Luân Đôn.

1676–1716. Phục vụ cho Gia tộc Hannover.

1677–98. Đình thần, ban đầu cho John Frederick, Công tước xứ Brunswick-Lüneburg, sau đó là cho em trai của ông này, Công tước (sau đó là Tuyển hầu tước) Ernst August của Hannover.

1687–90. Du lịch rộng khắp Đức, Áo, và Ý, nghiên cứu cho một cuốn sách mà Tuyển hầu tước đã thuê ông viết về lịch sử của Gia tộc Brunswick.

1698–1716: Quan viên trong cung đình của Tuyển hầu tước Georg Ludwig của Hannover.

1712–14. Tại thành Viên. Được đề cử làm Cố vấn Triều đình năm 1713 bởi Charles VI, Hoàng đế Thánh chế La Mã, tại triều đình Hapsburg ở Viên.

1714–16: Georg Ludwig, khi trở thành George I của Anh, đã cấm Leibniz không cho theo ông tới Luân Đôn. Leibniz trải qua những ngày cuối đời không ai chú ý tới.

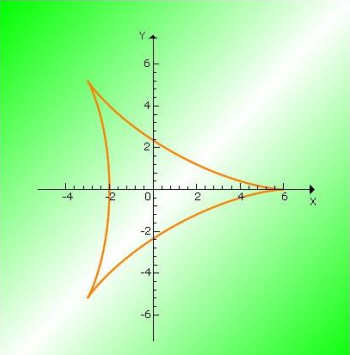
57. Tricuspoid (Đường cong Tricuspoid – Đường delta cong)

Phương trình đường cong trong hệ tọa độ Descartes:

$(x^{2}+y^{2})^{2}+18\cdot a^{2}(x^{2}+y^{2})-27a^{4}=8a\cdot (x^{3}-3xy^{2})$

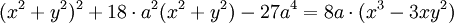
Phương trình tham số trong hệ tọa độ Descartes:

${\begin{cases}x=a(2\cos t+\cos 2t)\\y=a(2\sin t-\sin 2t)\end{cases}}$

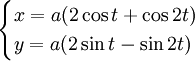
Phương trình đường cong trong hệ tọa độ cực:

$r^{4}+18\cdot a^{2}r^{2}-27\cdot a^{4}=8a\cdot r^{3}\cos 3\theta$

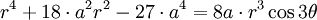
Tricuspoid hoặc deltoid lần đầu tiên được Euler nghiên cứu năm 1745, liên hệ với bài toán quang học. Steiner cũng khảo sát đường cong này năm 1856 nên còn được gọi là Steiner hypocycloid.

Chiều dài của tiếp tuyến với các tricuspoid, được đo giữa hai điểm P, Q, là 2 giao điểm của tiếp tuyến và đường cong là không đổi và bằng 4a.

Chiều dài của đường cong là 16a và diện tích giới hạn là $2\pi a^{2}$ .

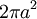Theo dạng tham số chỏm xảy ra tại t = 0, 2π / 3 và 4π / 3. Lưu ý sự giống nhau giữa các dạng tham số của tricuspoid và dạng tham số của cardioid.

Điểm tụ quang của tricuspoid, trong đó các tia song song và theo hướng bất kỳ, là một astroid.

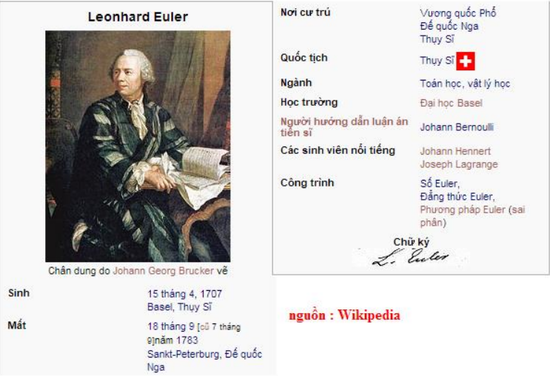
Leonhard Euler (15 tháng 4, 1707 – 18 tháng 9, 1783) là một nhà toán học và nhà vật lý học Thụy Sĩ. Ông (cùng với Archimedes và Newton) được xem là một trong những nhà toán học lừng lẫy nhất. Euler là người đầu tiên sử dụng từ "hàm số" (được Gottfried Leibniz định nghĩa trong năm 1694) để miêu tả một biểu thức có chứa các đối số, như y = F(x). Ông cũng được xem là người đầu tiên dùng vi tích phân trong môn vật lý.

Euler sinh và lớn lên tại Basel, và được xem là thần đồng toán học từ thưở nhỏ. Ông làm giáo sư toán tại Sankt-Peterburg, sau đó tại Berlin, rồi trở lại Sankt-Peterburg, là nhà toán học viết nhiều nhất: tất cả các tài liệu ông viết chứa đầy 75 tập, cũng là nhà toán học quan trọng nhất trong thế kỷ 18 và đã suy ra nhiều kết quả cho môn vi tích phân mới được thành lập. Euler bị mù hoàn toàn trong 17 năm cuối cuộc đời, nhưng khoảng thời gian đó là lúc ông cho ra hơn nửa số bài ông viết.

Tên của ông đã được đặt cho một miệng núi lửa trên Mặt Trăng và cho tiểu hành tinh 2002 Euler.

Các khám phá

1. Euler cùng với Daniel Bernoulli hoàn thành định luật, ở đó phát biểu rằng lực xoắn trên một sợi dây thun mỏng tỉ lệ với độ đàn hồi của vật liệu và mô men quán tính của mặt cắt. Ông đồng thời cũng đưa ra phương trình Euler, một tập hợp các định luật chuyển động trong thủy động lực học, quan hệ trực tiếp với định luật chuyển động của Newton. Những phương trình này có dạng tương đương với các phương trình Navier-Stokes với độ nhớt bằng 0.

2. Euler còn có đóng góp to lớn cho thuyết phương trình vi phân. Cụ thể, ông được biết đến nhiều với việc sáng tạo ra một chuỗi các phương pháp tính xấp xỉ, được sử dụng nhiều trong tinh toán. Và phương pháp nổi tiếng nhất trong đó chính là phương pháp Euler.

3. Trong lý thuyết số ông đã sáng tạo ta hàm totient. Totient của một số nguyên dương n được định nghĩa là số các số nguyên dương nhỏ hơn hoặc bằng n và nguyên tố cùng nhau với n. Ví dụ là 4 số 1, 3, 5, 7 đều là số nguyên tố nhỏ hơn 8.

4. Trong ngành giải tích, Euler đã tổng hợp hóa tích phân Leibniz với phương pháp tính Newton thành một dạng, gọi là vi phân. Năm 1735 ông hoàn thành cơ sở lý thuyết giải quyết bài toán Basel, vấn đề đã tồn tại trong một thời gian dài.

5. Một biểu thức nổi tiếng trong toán học, liên hệ giữa hàm mũ phức và hàm số lượng giác, hay còn gọi là đồng nhất thức Euler:

6. Năm 1735, ông tìm ra hằng số Euler-Mascheroni, được sử dụng rất nhiều trong các phương trình vi phân.

7. Ông là người cùng khám phá ra công thức Euler-Maclaurin, là một công cụ rất quan trọng trong việc tính toán các tích phân phức tạp, các tổng và chuỗi phức tạp.

8. Trong hình học và topo đại số có công thức Euler, liên hệ giữa các cạnh, đỉnh và mặt của một đa diện. Công thức tổng quát đó là: F - E + V = 2, ở đó F là số mặt, E là số cạnh và V là số đỉnh.

9. Năm 1736, Euler giải quyết bài toán nổi tiếng 7 chiếc cầu Königsberg, chính xác hơn, ông chứng minh bài toán không có đáp số. Kết quả được công bố trên bài báo nhan đềSolutio problematis ad geometriam situs pertinentis, và đó chính là ứng dụng sớm nhất của lý thuyết đồ thị hay của topology.

Tác phẩm

Euler có khối lượng sách viết đồ sộ nhưng những cuốn sách nổi tiếng nhất của bao gồm:

• Elements of Algebra (Nhập môn Đại số học). Cuốn sách về đại số căn bản này bắt đầu bàn một lời bàn luận về bản chất các con số và một lời giới thiệu tổng quan về đại số, bao gồm các công thức dành cho cách giải phương trình đa thức.

• Introductio in analysin infinitorum (1748): Nhập môn về giải tích vô cùng bé.

• Hai cuốn sách có ảnh hưởng về vi tích phân: Institutiones calculi differentialis Phép tính vi phân (1755) và Institutiones calculi integralisPhép tính tích phân (1768–1770).

• Principia motus fluidorum (1761): Nguyên lý chuyển động của chất lưu; cuốn sách trình bày phương trình liên tục và phương trình Euler.

• Lettres à une Princesse d'Allemagne (Lá thư gửi một Quận chúa Đức) (1768–1772). Có trực tuyến (bằng tiếng Pháp). Bản dịch tiếng Anh, có ghi chú, và cuộc đời của Euler có trực tuyến tại Google Books: Tập 1, Tập 2

• Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici latissimo sensu accepti (1744). Tựa đề Latin dịch là Phương pháp tìm những đường cong có tính chất cực đại hoặc cực tiểu, hoặc lời giải cho bài toán đẳng cấu trong chừng mực chấp nhận rộng rãi nhất.

Jakob Steiner sinh ngày 18 tháng 3, 1796 là con của Anna Barbara Weber (1757-1832) và Niklaus Steiner (1752-1826) trong gia đình tám người con. Jakob là con út, suốt thời thơ ấu ông phụ giúp cha mẹ mình làm việc tại các trang trại nhỏ và công việc kinh doanh. Dù không được học đọc và viết cho đến năm 14 tuổi, nhưng ông đã tỏ ra có những năng lực hơn người. Tuy vậy Jakob lại muốn làm một điều gì đó tốt hơn cho bản thân mình, trong khi cha mẹ ông rất hài lòng về sự giúp đỡ của ông với công việc nhà. Ở tuổi 18, Jakob Steiner quyết định rời nhà đến học tại trường Johann Heinrich Pestalozzi xứ Yverdom.

Môi trường này đã có một tác động rất đáng kể về thái độ của Steiner trong việc giảng dạy toán học và triết lý của ông khi thực hiện nghiên cứu toán học. Vào mùa thu năm 1818, Steiner rời Yverdom và đến Heidelberg. Ông đã tham dự các bài giảng tại các trường Đại học Heidelberg về giải tích tổ hợp, vi tích phân và đại số. Cũng vào thời gian này, ông đã bắt đầu quan tâm đến cơ học, đã viết ba bản thảo chưa được xuất bản về chủ đề này năm 1821, năm 1824 và 1825. Năm 1825, Steiner được bổ nhiệm làm trợ giảng tại Trường Kỹ thuật Berlin.

Vào năm 1832, Steiner xuất bản cuốn sách đầu tiên của ông " Systematische Entwicklung der Abhangigkeit geometrischer Gestalten voneinander " (Hệ thống phát triển về sự phụ thuộc của các dạng hình học). Phần lớn tư liệu đã xuất hiện trong các bài báo của Steiner trong sáu năm trước đó. Lời nói đầu của cuốn sách này cung cấp cho một cái nhìn thú vị về cách tiếp cận của Steiner đối với toán học nói chung và tư liệu hình học của cuốn sách nói riêng.

Chẳng bao lâu sau Steiner đã được vinh danh vì những thành tích vượt trội của mình. Ông được trao bằng tiến sĩ danh dự của trường Đại học Königsberg vào ngày 20 tháng 4 năm 1833 theo đề nghị của Jacobi, sau đó được bầu vào Viện Hàn lâm Khoa học Phổ vào ngày 05 Tháng Sáu năm 1834. Jakob Steiner được bổ nhiệm làm giáo sư về bộ môn hình học tại Đại học Berlin vào ngày 08 tháng 10, 1834. Ông đến Rome vào năm 1844 và trong chuyến thăm này, ông đã dành thời gian nghiên cứu mặt bậc 4 thuộc lớp thứ ba - danh từ chuyên ngành hiện đại gọi là ' mặt Roman ' hoặc 'mặt Steiner'. Ông đã trải qua mùa đông 1854-55 tại Paris và trong thời gian đó ông được bầu vào Académie des Sciences (Pháp).

Ông là một trong những người có đóng góp lớn nhất đối với bộ môn hình học xạ ảnh. Ông phát hiện ra 'mặt Steiner',- là bề mặt trong đó có một số vô hạn kép các tiết diện conic trên nó. Một kết quả nổi tiếng khác là "định lý Poncelet-Steiner" trong đó cho thấy rằng chỉ cần có một đường tròn và đường thẳng cho các cấu trúc hình học Euclide.

Mười năm cuối cùng của cuộc đời của Steiner đầy dẫy khó khăn bệnh tật. Căn bệnh về thận khiến ông phải mất nhiều thời gian điều trị ở Thụy Sĩ, ông chỉ đến Berlin vào các mùa đông để cung cấp các bài giảng của mình. Cuối cùng, vì bệnh quá nặng ông đã hoàn toàn nằm liệt giường và không thể thực hiện nhiệm vụ giảng dạy được nữa. Steiner không lập gia đình vì thế toàn bộ tài sản của ông đều dành cho khoa học và từ thiện. Một phần ba của tài sản này đã trao cho Viện Hàn lâm Berlin để thành lập giải thưởng Steiner. Phần còn lại được chia cho người thân của ông và các trường học ở quê hương Utzenstorf. Mong muốn cuối cùng của Jakob Steiner là trẻ em nghèo ở quê nhà có thể có được một cơ hội giáo dục tốt hơn so với bản thân ông đã có.

Hình dạng tricuspoid có trong thế giới tự nhiên

58. Trident of Newton (Đường hình xiên Newton)

Phương trình đường cong trong hệ tọa độ Descartes: $x\cdot y=cx^{3}+dx^{2}+ex+f$

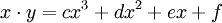
Đường cong này đã được Newton và Descartes khảo sát. Đôi khi nó được gọi là 'Parabola Descartes' mặc dù nó không phải là một parabol. Đường hình xiên là tên gọi do Newton đề xuất trong công trình nghiên cứu các hàm bậc 3 Curves, tuyển tập Lexicon Technicum của Sir Isaac Newton, NXB John Harris xuất bản tại London năm 1710.

Newton là người đầu tiên đã thực hiện nghiên cứu hệ thống hóa các phương trình bậc ba và ông đã phân loại chúng thành 72 trường hợp khác nhau. Trong thực tế, ông đã bỏ qua sáu trường hợp trong hệ thống phân loại của mình. Đường hình xiên là dạng thứ 66 trong phân loại này và Newton cung cấp các đồ thị về cơ bản giống với đồ thị đưa ra ở trên.

Newton cũng nêu một số đặc tính của đường cong hình xiên. Ví dụ, ông nói rằng đường cong có bốn nhánh vô hạn mà trục y là một tiệm cận đứng.

Việc phân loại của các hàm bậc 3 của Newton đã bị Euler chỉ trích vì nó thiếu các nguyên tắc chung. Plücker sau đó đã đưa ra một phân loại chi tiết hơn với 219 loại.

Isaac Newton (1642 - 1727) - nhà vật lý, toán học nước Anh, người được thế giới tôn là "người sáng lập ra vật lý học cổ điển"

Năm 17 tuổi, ông vào học ở trường Đại học tổng hợp Cambridge. Thời gian còn là sinh viên, Newton đã tìm ra nhị thức trong toán học giải tích, được gọi là "nhị thức Newton ". Năm 19 tuổi, ông bắt đầu nghiên cứu rộng rãi về khoa học tự nhiên.

Năm 27 tuổi, Newton được cử làm giáo sư toán ở trường Đại học nơi ông học; năm 30 tuổi, ông được bầu làm hội viên Hội khoa học hoàng gia Anh (Viện hàn lâm) và 23 năm cuối đời, ông làm chủ tịch Hội khoa học hoàng gia Anh. Newton còn là hội viên danh dự của nhiều Hội khoa học và viện sĩ của nhiều Viện hàn lâm.

Thành tựu khoa học của ông trên nhiều lĩnh vực, phép tính vi tích phân ông sáng lập là một cột mốc trong lịch sử toán học; giải thích về các loại màu sắc của vật thể đã mở đường sáng lập khoa học quang phổ. Cống hiến lớn khiến tên tuổi Newton trở thành bất tử là " Ba định luật về chuyển động " đặt cơ sở lý luận cho lực học kinh điển, quan trọng nhất là "Nguyên lý vạn vật hấp dẫn". Đây là nguyên lý cơ sở cho những phát minh vật lý học, cơ học, thiên văn học trong nhiều thế kỷ.

Newton mất năm 84 tuổi. Ông được mai táng ở Đài kỷ niệm quốc gia Anh trong tu viện Westminster - nơi an nghỉ của các vua chúa và các bậc vĩ nhân của nước Anh.

Julius Plücker là một nhà toán học người Đức, người đã có những đóng góp quan trọng về hình học giải tích và vật lý.

Gia đình Julius Plücker có nguồn gốc từ các thương gia sống tại Aachen. Plücker học tại Gymnasium, Düsseldorf, sau khi tốt nghiệp, ông tiếp tục theo học tại một số trường đại học khác nhau. Ông lần đầu tiên tham dự Đại học Bonn, sau đó đến Heidelberg trước khi đi du học tại Berlin. J. Plücker đến Pháp vào năm 1823, nơi ông tham dự các khóa học về hình học tại Đại học Paris. Ông đã hoàn thành luận án tiến sĩ năm 1823 với Giáo sư cố vấn luận án là Christian Gerling tại Marburg. Ông đã gửi luận án Habil của mình đến Đại học Bonn vào năm 1824 và được bổ nhiệm làm trợ lý giáo sư, sau đó Julius Plücker được phong giáo sư tại Bonn vào năm 1828,

Tuy Plücker là một nhà hình học nhưng ông tin tưởng chắc chắn vào tầm quan trọng của các ứng dụng của toán học với khoa học vật lý. Năm 1847, ông đã chuyển sang vật lý tại đại học Bonn bắt đầu nghiên cứu về từ tính, điện tử và vật lý nguyên tử. Ông dự đoán trước cả Kirchhoff và Bunsen về các vạch phổ đặc trưng cho từng chất hóa học.

Tác phẩm lớn đầu tiên của ông là " Analytisch-geometrische Entwickelungen" đã được xuất bản thành hai tập, lần đầu tiên vào năm 1828 và ba năm sau in tiếp tập thứ hai. Tác phẩm lớn tiếp theo của ông là " System der analytischen Géométrie, auf neue Betrachtungsweisen gegrundet, und insbesondere eine ausführliche Theorie der Kurven dritter Ordnung enthaltend " (1835) đề cập điểm và tọa độ đường thẳng áp dụng cho bài toán tiết diện conic. Phần chính của công trình này là thảo luận về đường cong bậc 3 trong mặt phẳng.

Vào năm 1868, Plücker xuất bản phần đầu tiên của " Neue Geometrie des Raumes, gegründet auf die Betrachtung der geraden Linie als Raumelement " nhưng ông mất trước khi phần thứ hai đã được hoàn tất. Klein là trợ lý của ông trước đó đã thảo luận những ý tưởng mà Plücker nhằm phát triển trong phần thứ hai này. Klein sau đó thực hiện kế hoạch như dự kiến của Plücker và phát hành tập thứ hai vào năm 1869.

Julius Plücker đã được tặng thưởng Huân chương Copley của Hội Hoàng gia vào năm 1866.

Tham khảo

1. http://www-history.mcs.st-andrews.ac.uk/Curves/Curves.html

2. http://www-history.mcs.st-andrews.ac.uk/

3. Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers. Department of Mathematics, Computer Science, and Statistics,Bloomsburg University

4. Bloomsburg, Pennsylvania 17815. 4. A Handbook on curves and their properties. Robert C. Yates, printed by Edwards Brothers, Inc - Ann Arbor, Michigan U.S.A.

5. http://www.slideshare.net/guest3f32c32/ncurving-a-transformation-of-curves?ref=

Bản quyền

Trần Hồng Cơ

Biên tập và trích dịch.

Ngày 01/04/2012

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

Mục lục

1. Giới thiệu
2. Phần 1. Từ As đến Co (1 – 10)
3. Phần 2. Từ Co đến Eq (11 – 21)
4. Phần 3. Từ Fe đến Ka (22 – 32)
5. Phần 4. Từ Ka đến Pa (33 – 42)
6. Phần 5. Từ Pe đến Rh (43 – 48)
7. Phần 6. Từ Ri đến Sp (49 – 53)
8. Phần 7. Từ Sp đến Tr (54 – 58)
9. Phần 8. Từ Tr đến Wi (59 – 63)

Bài liên quan

• Tỉ lệ logarit
• Vai trò công cụ của logarit qua một số ứng dụng
• Vài nét sơ lược về lịch sử xuất hiện khái niệm logarit
• Vấn đề dạy học logarit trong chương trình toán phổ thông và những điều cần biết về logarit
• Kẻ thất bại và kẻ siêu thất bại

• « Mới nhất
• ‹ Mới hơn
• Cũ hơn ›

Liên kết đến đây

• Danh mục và lịch sử các đường cong
• Bản mẫu:Danh mục và lịch sử các đường cong
• Danh mục và lịch sử các đường cong/Phần 1. Từ As đến Co (1 – 10)
• Danh mục và lịch sử các đường cong/Phần 2. Từ Co đến Eq (11 – 21)
• Danh mục và lịch sử các đường cong/Phần 3. Từ Fe đến Ka (22 – 32)
• Danh mục và lịch sử các đường cong/Phần 4. Từ Ka đến Pa (33 – 42)
• Danh mục và lịch sử các đường cong/Phần 5. Từ Pe đến Rh (43 – 48)
• Danh mục và lịch sử các đường cong/Phần 6. Từ Ri đến Sp (49 – 53)
• Danh mục và lịch sử các đường cong/Phần 8. Từ Tr đến Wi (59 – 63)