Danh mục và lịch sử các đường cong/Phần 8. Từ Tr đến Wi (59 – 63)

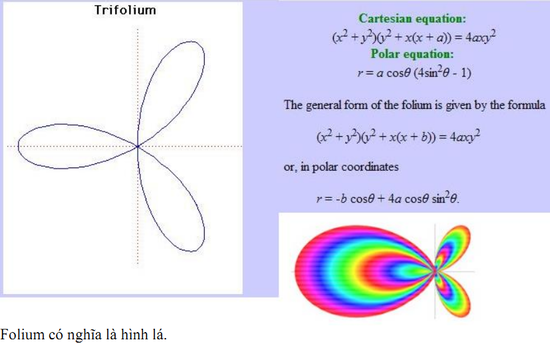
59. Trifolium (Đường hoa 3 cánh)

Phương trình đường cong trong hệ tọa độ Descartes: $(x^{2}+y^{2})(y^{2}+a\cdot x+x^{2})=4axy^{2}$

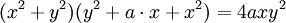
Phương trình đường cong trong hệ tọa độ cực: $r=a\cos \theta \cdot (4\sin ^{2}\theta -1)$

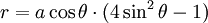
Trường hợp tổng quát

Phương trình đường cong trong hệ tọa độ Descartes: $(x^{2}+y^{2})(y^{2}+b\cdot x+x^{2})=4axy^{2}$

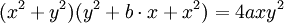
Phương trình đường cong trong hệ tọa độ cực: $r=-b\cos \theta a+4a\cos \theta \cdot \sin ^{2}\theta$

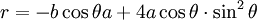
Có ba dạng đặc biệt của các folium, folium đơn, folium đôi và Trifolium. Những đường cong trên tương ứng với các trường hợp b = 4a, b = 0, b = a

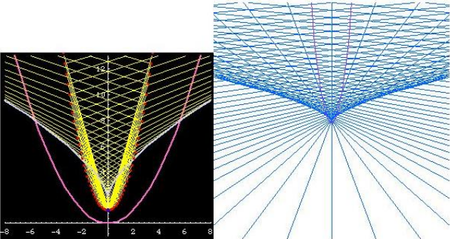
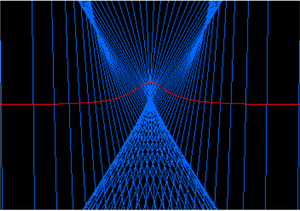
Đồ thị vẽ ở trên là Trifolium.

Minh họa về đường pháp bao ngoài của trifolium

Hình:TRIFOLIUM.gif

Đọc thêm về các tính chất của đường hoa 3 cánh. http://www.slideshare.net/cohtran/trifolium?ref=

Mã nhúng:

<iframe src="http://www.slideshare.net/slideshow/embed_code/14353408" width="479" height="511" frameborder="0" marginwidth="0" marginheight="0" scrolling="no" style="border:1px solid #CCC; border-width:1px 1px 0; margin-bottom:5px; max-width: 100%;" allowfullscreen></iframe>

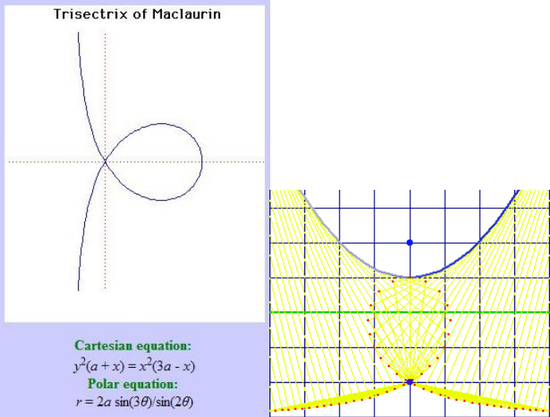
60. Trisectrix of Mac Laurin (Đường phân ba góc Mac Laurin)

Phương trình đường cong trong hệ tọa độ Descartes: $y^{2}(\ a+x)=x^{2}(3a-x)$

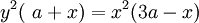
Phương trình đường cong trong hệ tọa độ cực: $r={\frac {2a\sin 3\theta }{\sin 2\theta }}$

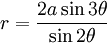
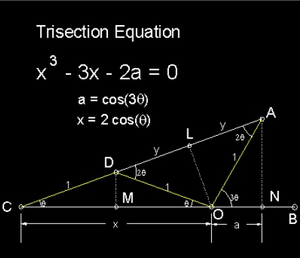
Đường cong này lần đầu tiên được Colin Maclaurin nghiên cứu vào năm 1742. Giống như rất nhiều các đường cong khác nó đã được nghiên cứu để cung cấp lời giải cho một trong những bài toán Hy Lạp cổ đại, liên quan đến bài toán phân 3 (trisecting) một góc. Trisectrix là tên phát sinh kể từ khi nó có thể được sử dụng để chia một góc làm ba phần bằng nhau. Phương trình phân ba góc có dạng đại số như sau đây:

Các đường phân ba góc (trisectrix) Maclaurin là một đường cong anallagmatic.

Một dạng khác của phương trình là 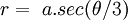$r=\ a.sec(\theta /3)$ , trong đó gốc nằm trong vòng lặp và giao điểm trên nửa trục x âm .

Các tiếp tuyến với đường cong tại gốc tạo thành những góc 60° với trục x.

Diện tích của vòng lặp là 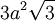$3a^{2}{\sqrt {3}}$ và khoảng cách từ gốc đến điểm mà đường cong cắt trên trục x là 3a.

Xem Đường phân ba góc (trisectrix) Maclaurin là một đường cong anallagmatic.

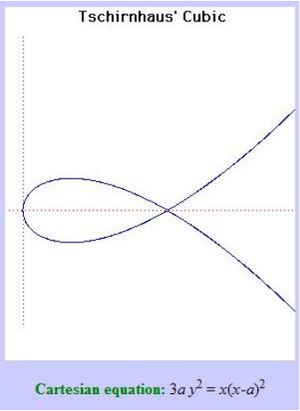
61. Tschirnhaus’ Cubic (Đường bậc 3 Tschirnhaus)

Phương trình đường cong trong hệ tọa độ Descartes: $3a\cdot y^{2}=x(x-a)^{2}$

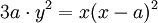
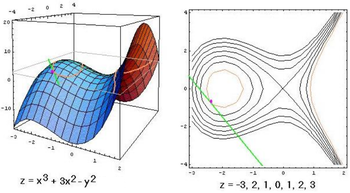
Đường cong này đã được Tschirnhaus, de L'Hôpital và Catalan nghiên cứu. Cũng như đường bậc 3 Tschirnhaus, đôi khi nó còn được gọi là đường bậc 3 de L'Hôpital's hoặc đường phân ba góc -trisectrix - Catalan.

Tên đường bậc 3 Tschirnhaus được RC Archibald chính thức đưa ra trong các văn bản vào năm 1900, trong lúc ông đã cố gắng sắp xếp và phân loại các đường cong.

Điểm tụ quang của đường bậc 3 Tschirnhaus là nơi mà điểm radiant là cực của parabole nửa- bậc- 3 Neile – (Neile's semi-cubic parabola).

Điểm tụ quang của đường bậc 3 Tschirnhaus

Ehrenfried Tschirnhaus là một nhà toán học người Đức, người đã khảo sát các lời giải của phương trình và nghiên cứu tính chất các đường cong. Ông được biết đến về phép biến đổi mà loại bỏ các số hạng bậc n-1 từ một phương trình bậc n.

Ehrenfried Walter von Tschirnhaus (hoặc Tschirnhausen) được sinh ra trong Kieslingswalde ở Đức, nhưng kể từ năm 1945, thị trấn đổi tên thành Slawnikowice thuộc miền tây Ba Lan. Ông là con trai út và đứa con thứ bảy của Christoph von Tschirnhaus và Elisabeth Eleonore Freiin Achyll von Stirling. Christoph là địa chủ xuất thân từ giới quý tộc Saxon trong khi Elisabeth là có nguồn gốc từ Đức và Scotland, có họ xa với gia đình Stirling có năng khiếu toán học.

Khi Tschirnhaus lên sáu tuổi mẹ ông qua đời nhưng bù lại ông được người mẹ kế rất yêu thương. Năm 1666, ông vào Gymnasium ở Görlitz, nơi ấy ông đã dành hai năm chuẩn bị cho đại học. Ông có mối quan tâm sâu sắc trong toán học ở giai đoạn này. Tschirnhaus tự tham khảo những bài học riêng trong các chủ đề toán học và điều này khiến kiến thức của ông vượt xa các tư liệu ở trường.

Tschirnhaus vào Đại học Leiden vào mùa thu của 1668 và ở đó ông học toán học, triết học, vật lý và y học. Ông cũng trúng tuyển giảng viên luật tại Leiden vào ngày 8 tháng Sáu 1669 nhưng có vẻ như ông không quan tâm nhiều đến việc đó. Ông đã tiếp thu được những tiến bộ mới nhất trong y học như lý thuyết của Harvey liên quan đến vòng tuần hoàn máu. Ông cũng theo học Pieter van Schooten (anh trai kế của nhà toán học nổi tiếng Frans van Schooten) và đã được giới thiệu về toán học và triết học của Descartes.

Với một thư giới thiệu của Spinoza, Tschirnhaus viếng thăm Anh tháng 5 năm 1675 nơi ông đã gặp Oldenburg thư ký của Hội Hoàng gia. Oldenburg đã giới thiệu ông với những bác học nổi tiếng khác, Robert Boyle, Denis Papin, và Isaac Newton. Ông cũng đã gặp John Collins ở London và John Wallis tại Oxford. Ông đã trình cho Collins và Wallis các phương pháp giải phương trình, nhưng hóa ra đây lại là trường hợp đặc biệt của một kết quả nghiên cứu đã được biết đến. Với một lá thư giới thiệu từ Oldenburg, ông đến Paris vào mùa thu năm 1675, nơi ông ở lại trong một thời gian sau khi gặp Leibniz và Huygens.

Tháng 11 năm 1676, ông rời Paris, đi cùng Bá tước Nimpsch xứ Silesia. Họ lần đầu tiên đến Lyon, nơi Tschirnhaus gặp lại Villette và cùng tiến hành các thí nghiệm vật lý. Sau đó Tschirnhaus đến Turin, Milan, Venice, Bologna và Rome. Ở khắp mọi nơi đã đi, ông đều liên lạcvà tiếp xúc với các nhà khoa học hàng đầu thế giới bao gồm cả Athanasius Kircher và Alfonso Borelli ở Rome. Tschirnhaus tiếp tục đến thăm Naples, Sicily, Milan, và Geneva trước khi trở về năm 1679 Paris, The Hague (nơi ông đến thăm Huygens) và Hanover (nơi ông đến thăm Leibniz). Trong khi thực hiện cuộc hành trình dài này, Tschirnhaus thường xuyên báo cáo quan sát và khám phá của mình cho Leibniz bằng thư, và nhận được nhiều phản hồi hữu ích. Ví dụ, ngày 30 tháng tư năm 1678 Tschirnhaus đã viết một lá thư dài cho Leibniz từ Rome. Trong đó ông đã thảo luận một số câu hỏi toán học bao gồm các lời giải của phương trình bậc cao. Ông đề nghị rằng nên xem đại số như là một môn học có chủ đề rộng và bao quát, trong đó tổ hợp chỉ là một phần trong môn này. Sau khi kết thúc cuộc hành trình dài của mình năm 1679, Tschirnhaus sống ở quê nhà Kieslingswalde trong suốt một thời gian dài. Tschirnhaus tiếp tục thực hiện một chuyến thăm thứ ba đến Paris năm 1682, và tại đây vào ngày 22 tháng 7, ông được bầu vào Académie des Sciences.

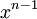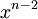Tschirnhaus khảo sát các lời giải của phương trình và nghiên cứu tính chất các đường cong. Ông đã phát hiện ra phép biến đổi, khi áp dụng cho một phương trình bậc n, sẽ dẩn về một phương trình bậc n không có số hạng $x^{{n-1}}$ và $x^{{n-2}}$ . Ông cũng nghiên cứu các đường cong catacaustic năm 1682, những là chùm của các tia sáng phát ra từ một nguồn điểm sau khi phản xạ từ một đường cong cho trước. Công trình của ông về các đường cong này được nhớ đến với một đường xoắn ốc hình sin được mang tên Tschirnhaus.

Vào năm 1700 Tschirnhaus xuất bản tác phẩm " Gründliche Anleitung zu nützlichen Wissenschaften "rất được Leibniz ca ngợi và ảnh hưởng rất lớn đến Christian Wolff sau này.

Đường bậc 3 Tschirnhaus là hình chiếu của mặt cong trên mặt phẳng tọa độ z = 0

Đọc thêm về các tính chất của đường bậc 3 Tschirnhaus http://www.slideshare.net/cohtran/tschirnhaus?ref=

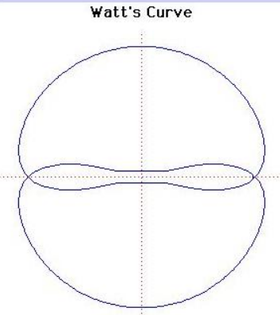
62. Đường cong Watt

Phương trình đường cong trong hệ tọa độ cực: $r^{2}=b^{2}-[a\sin \theta \pm {\sqrt {c^{2}-a^{2}\cos ^{2}\theta }}]^{2}$

Phương trình đường cong trong hệ tọa độ Descartes:

$(x^{2}+y^{2})(x^{2}+y^{2}-d^{2})^{2}+4a^{2}y^{2}(x^{2}+\ y^{2}-b^{2})=0$

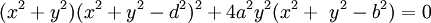
với $d^{2}=a^{2}+\ b^{2}-c^{2}$

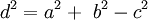
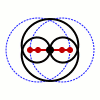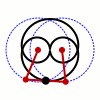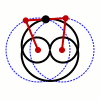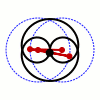
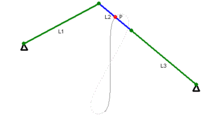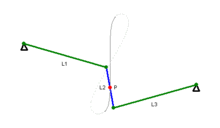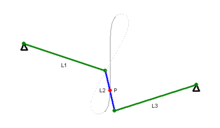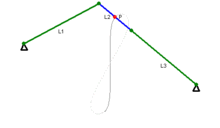
Trong toán học, đường cong Watt là một đường cong đại số phẳng bậc 6. Nó được tạo ra bởi hai đường tròn bán kính b, khoảng cách giữa 2 tâm I(±a, 0) bằng 2a. Một đoạn thẳng độ dài 2c gắn vào một điểm trên mỗi vòng tròn, và trung điểm của đoạn thẳng đó vẽ ra đường cong Watt khi các đường tròn xoay. Đường cong này có liên quan với công trình nghiên cứu tiên phong về động cơ hơi nước của James Watt, được đặt tên sau khi James Watt (1736 - 1819), kỹ sư người Scotland, người đã phát triển động cơ hơi nước. Trong thực tế, đường cong xuất phát từ các mối liên kết của các thanh kết nối hai bánh xe có đường kính bằng nhau.

Sylvester, Kempe và Cayley tiếp tục phát triển hình học kết hợp với các lý thuyết về các liên kết trong những năm 1870. Thực tế Kempe đã chứng minh rằng tất cả các đoạn hữu hạn của một đường cong đại số có thể được tạo ra bởi một mối liên kết theo cách này. Nếu a = c thì C là một đường tròn bán kính b với số 8 bên trong nó.

Sir Alfred Bray Kempe D.C.L (Tiến sĩ luật) -F.R.S (thành viên Hội hoàng gia Anh) (6 1849, Kensington, Luân Đôn - 21 Tháng Tư 1922, London) là một nhà toán học nổi tiếng nhất về công trình mối liên kết và các định lý bốn màu.

Kempe học tại Trinity College, Cambridge, nơi Arthur Cayley là một trong những giáo viên nổi tiếng đã giảng dạy cho ông. Ông tốt nghiệp cử nhân (22 wrangler) vào năm 1872. Mặc dù quan tâm chính của ông là toán học, nhưng ông lại trở thành một luật sư, chuyên về pháp luật của Giáo Hội. Ông được phong tước hiệp sĩ vào năm 1913, năm đó ông trở thành Chancellor cho Giáo Phận London. Ông đã nhận được bằng danh dự D.C.L. (Doctor of Canon Law (Latin: Juris Canonici Doctor; J.C.D.) học vị thuộc Giáo hội La mã)từ Đại học Durham.

Năm 1877 Kempe phát hiện ra mối liên kết đoạn thẳng mới và đã xuất bản các bài giảng có ảnh hưởng về đề tài này. Định lý Kempe tổng quát về các liên kết phát biểu rằng bất kỳ tập hợp con bị chặn nào của một đường cong đại số có thể được phác thảo ra bởi sự chuyển động của một trong các khớp nối trong một mối liên kết được lựa chọn thích hợp. Cách chứng minh của Kempe ban đầu là sai lầm, và được các nhà toán học chứng minh lần đầu tiên hoàn chỉnh vào năm 2002, dựa trên ý tưởng của ông.

Năm 1879, Kempe đã đưa ra " chứng minh " nổi tiếng của ông về định lý bốn màu, nhưng Percy Heawood chỉ ra sự không chính xác của nó vào năm 1890. Mãi về sau, công trình của ông đã dẫn đến các khái niệm cơ bản như chuỗi Kempe và các tập hợp tất yếu.

Về các lĩnh vực triết học năm 1886 Kempe đã khai mở một khuynh hướng mới đáng lưu ý, và nhiều tạo ra nhiều ảnh hưởng đến Charles Sanders Peirce. Kempe cũng phát hiện ra những khái niệm mà bây giờ được gọi là đa tập hợp -multisets, mặc dù thực tế này đã không được ghi nhận cho đến khá lâu sau khi ông mất. Kempe đã được bầu làm thành viên của Hội Hoàng gia vào năm 1881. Ông là chủ tịch của Hội Toán học London từ 1892 đến 1894. Ông cũng là một nhà leo núi, chủ yếu là ở Thụy Sĩ.

Arthur Cayley F.R.S. (thành viên Hội hoàng gia Anh) (phiên âm: / 'Keɪli /; Tháng Tám 16, 1821 - 26 tháng một năm 1895) là một nhà toán học người Anh. Ông là người đã góp công lớn trong việc xây dựng các trường phái toán học thuần túy hiện đại Anh..

Khi còn nhỏ, Cayley rất thích giải quyết các vấn đề toán học phức tạp thiên về giải trí. Ông đã học tại Trinity College, Cambridge, và tỏ ra rất xuất sắc về tiếng Hy Lạp, tiếng Pháp, tiếng Đức, và Ý, cũng như toán học. Ông làm việc trong vai trò luật sư trong 14 năm.

Ông đưa ra định lý Cayley-Hamilton, rằng tất cả các ma trận vuông là nghiệm của đa thức đặc trưng của riêng nó, và chứng minh điều này cho ma trận vuông cấp 2 và 3. Arthur Cayley cũng là người đầu tiên xác định khái niệm của một nhóm theo cách nhìn hiện đại - như là một tập hợp với một phép toán hai ngôi thỏa mãn một định luật nào đó. Trước đây, khi các nhà toán học đã nói về "nhóm", họ thường hiểu nghĩa là các nhóm hoán vị.

63. Witch of Agnesi (Đường cong phù thủy Agnesi)

Phương trình đường cong trong hệ tọa độ Descartes: $y(x^{2}+\ a^{2})=a^{3}$

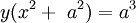
Phương trình đường cong trong hệ tọa độ cực: ${\begin{cases}x=at\\y={\frac {a}{1+t^{2}}}\end{cases}}$

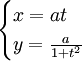
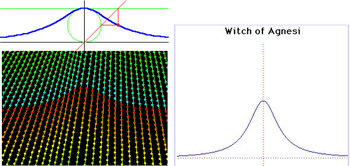
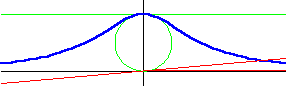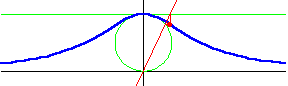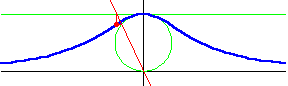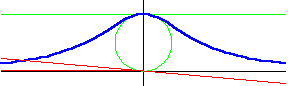
Đường cong này đã được Maria Agnesi nghiên cứu và đặt tên là versiera năm 1748 trong cuốn sách của cô có tên là " Istituzioni Analitiche ". Nó còn được gọi là đường bậc 3 Agnesi - Cubique d'Agnesi hoặc Agnésienne. Đã có một cuộc thảo luận thú vị về lý do để đường cong này được gọi là đường phù thủy trong cuốn sách tiểu sử Agnesi. Đường cong đã được Fermat và Guido Grandi nghiên cứu trước đó vào năm 1703.

Đường cong nằm giữa y = 0 và y = a. Nó có điểm uốn tại y = 3a / 4. Đường thẳng y = 0 là một tiệm cận đường cong.

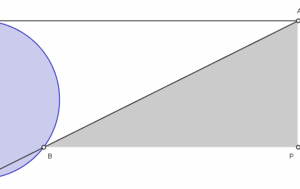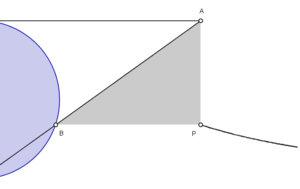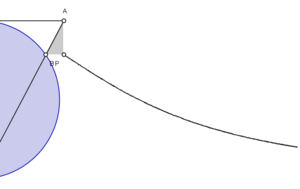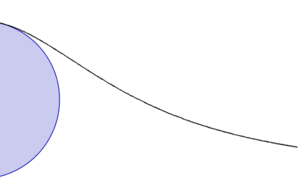
Đường cong có thể được coi như một quỹ tích của một điểm P được xác định như sau. Vẽ một đường tròn C có tâm tại (0, a / 2) đi qua gốc O. Dựng đường thẳng từ O cắt C tại L và đường thẳng y = a tại M. Khi đó, P có x-tọa độ của M và toạ độ y của L. Tiếp tuyến với đường cong phù thủy Agnesi tại điểm với tham số p là $(p^{2}+1)^{2}\ y+2px=a(3p^{2}+1)$

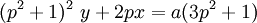
Maria Agnesi là một nhà toán học người Ý được ghi nhận là có công trình đóng góp trong phép tính vi phân. Cô đã từng khảo sát về đường cong bậc ba bây giờ được biết như là " đường phù thủy của Agnesi ”.

Maria Gaetana Agnesi (sinh ngày 16 tháng 5 năm 1718 - mất ngày 09 tháng 01 năm 1799) là một nhà toán học và triết học người Ý.

Cô được coi là người viết cuốn sách đầu tiên thảo luận về cả hai lĩnh vực vi phân và tích phân và là một thành viên danh dự trong đội ngũ các giảng viên tại Đại học Bologna, Ý.

Điểm đáng trân trọng là cô đã dành bốn thập niên cuối cùng của cuộc đời mình để nghiên cứu thần học (đặc biệt là patristics) và phục vụ tầng lớp người nghèo. Maria Gaetana Agnesi được sinh ra tại Milan vào ngày 16 tháng năm 1718, trong một gia đình giàu có và có học thức. Cha cô vì muốn nâng cao vị thế gia đình của mình vào giới quý tộc Milan và để đạt được mục tiêu của mình, ông đã kết hôn năm 1717 với Anna Fortunata Brivio, một thiếu nữ thuộc lớp thượng lưu. Cái chết của mẹ cô đã tạo cho cô cái cớ để rút lui khỏi cộng đồng giới quyền quý. Maria Gaetana Agnesi lúc này trở thành người quản lý công việc của gia đình.

Từ khi sinh ra tại Milan, Maria đã được công nhận như là một thần đồng từ rất sớm, cô có thể nói cả Ý và Pháp lúc năm tuổi. Ngày sinh nhật thứ 13 của Maria Gaetana Agnesi, cô đã có thể nói lưu loát được tiếng Hy Lạp, Do Thái, Tây Ban Nha, Đức, và cả tiếng Latin, thường được gọi là "thần đồng ngôn ngữ". Cô thậm chí còn có thể dạy ngôn ngữ cho cả các anh em trai của mình. Khi lên 9 tuổi, Maria Gaetana Agnesi đã sáng tác và đọc một bài phát biểu kéo dài một giờ bằng tiếng Latin đến cử tọa là một số những trí thức nổi bật nhất đương thời. Các chủ đề cô thường nói là về quyền được giáo dục của phụ nữ.

Khi Maria lên mười lăm tuổi, cha của cô bắt đầu thường xuyên tụ tập tại nhà của ông một nhóm gồm những học giả nổi tiếng nhất ở Bologna, những người mà trước đây cô đã từng có dịp đọc các tác phẩm và trao đổi một loạt đề tài về các vấn đề triết học sâu sắc nhất. Ghi nhận về các cuộc họp này được lưu lại trong cuốn " Charles de Brosses Lettres sur l'Italie và Philosophicae Propositiones ", mà sau đó cha cô đã xuất bản năm 1738. Trong thời gian đó, Maria bắt đầu nghiên cứu về vi phân và tích phân.

Công trình đáng giá nhất của Maria Gaetana Agnesi là tác phẩm " Instituzioni analitiche ad uso della gioventù italiana ", xuất bản tại Milan vào năm 1748, đây được coi là bản giới thiệu tốt nhất còn tồn tại cho đến nay về các công trình của Euler. Cuốn thứ nhất viết về giải tích đại lượng hữu hạn và cuốn thứ hai là về giải tích vô cùng bé - infinitesimals. Một bản dịch tiếng Pháp của tập thứ hai bởi P.T. d'Antelmy, với phần bổ sung của Charles Bossut (1730-1814), đã được xuất bản tại Paris năm 1775, và một bản dịch tiếng Anh của toàn bộ công trình của Maria Gaetana Agnesi bởi John Colson (1680-1760), được kiểm định bởi John Hellins - một nhà toán học tại Cambrige, cũng đã được xuất bản sau đó vào năm 1801. Trong tác phẩm " Instituzioni analitiche ad uso della gioventù italiana ", Maria Gaetana Agnesi đề cập đến các đường cong đã được khảo sát trước đó bởi Pierre de Fermat và Guido Grandi. Grandi gọi tên các đường cong này là versoria theo tiếng Latin và đề nghị gọi là versiera theo tiếng Ý, có lẽ do sự chơi chữ " versoria " trong thuật ngữ hàng hải có nghĩa là dây buồm, trong khi " versiera " theo tiếng Ý lại có nghĩa là Nữ quỷ (hay phù thủy). Vì thế sau khi dịch sang bản Anh ngữ đường cong versoria này có tên gọi là " witch of Agnesi "

Điểm tụ quang trên đường cong Agnesi

Agnesi cũng đã viết một bài bình luận cho cuốn " Traité analytique des sections coniques du marquis de l'Hôpital " mặc dù được đánh giá cao bởi những người đã từng đọc bản thảo này, nhưng đáng tiếc chưa bao giờ được công bố rộng rãi.

Năm 1750, Maria Gaetana Agnesi được Đức Giáo Hoàng Benedict XIV bổ nhiệm vào chức giáo sư toán học, triết học tự nhiên và vật lý tại Bologna. Cô là người phụ nữ đầu tiên được bổ nhiệm làm giáo sư tại một trường đại học Ý. Sau cái chết của cha mình năm 1752, cô quyết định thực hiện một mục đích đã được ấp ủ từ lâu là nghiên cứu thần học, đặc biệt là về các Giáo Phụ và cống hiến đời mình cho các bệnh nhân, người nghèo và vô gia cư. Sau vài năm giữ chức vụ giám đốc Trivulzio Hospice thuộc dòng nữ tu Thiên Thanh ở Milan, bản thân cô cũng tham gia dòng này. Cô đã sống những ngày tháng phục vụ rất khắc khổ cho đến cuối đời (ngày 09 tháng một năm 1799), mặc dù cho đến nay chưa ai được biết đầy đủ về cái chết của cô.

Tham khảo

1. http://www-history.mcs.st-andrews.ac.uk/Curves/Curves.html

2. http://www-history.mcs.st-andrews.ac.uk/

3. Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers. Department of Mathematics, Computer Science, and Statistics,Bloomsburg University

4. Bloomsburg, Pennsylvania 17815. 4. A Handbook on curves and their properties. Robert C. Yates, printed by Edwards Brothers, Inc - Ann Arbor, Michigan U.S.A.

5. http://www.slideshare.net/guest3f32c32/ncurving-a-transformation-of-curves?ref=

Bản quyền

Trần Hồng Cơ

Biên tập và trích dịch.

Ngày 01/04/2012

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 United States License.

Mục lục

1. Giới thiệu
2. Phần 1. Từ As đến Co (1 – 10)
3. Phần 2. Từ Co đến Eq (11 – 21)
4. Phần 3. Từ Fe đến Ka (22 – 32)
5. Phần 4. Từ Ka đến Pa (33 – 42)
6. Phần 5. Từ Pe đến Rh (43 – 48)
7. Phần 6. Từ Ri đến Sp (49 – 53)
8. Phần 7. Từ Sp đến Tr (54 – 58)
9. Phần 8. Từ Tr đến Wi (59 – 63)

Bài liên quan

• Tỉ lệ logarit
• Vai trò công cụ của logarit qua một số ứng dụng
• Vài nét sơ lược về lịch sử xuất hiện khái niệm logarit
• Vấn đề dạy học logarit trong chương trình toán phổ thông và những điều cần biết về logarit
• Kẻ thất bại và kẻ siêu thất bại

• « Mới nhất
• ‹ Mới hơn
• Cũ hơn ›

Liên kết đến đây

• Danh mục và lịch sử các đường cong
• Bản mẫu:Danh mục và lịch sử các đường cong
• Danh mục và lịch sử các đường cong/Phần 1. Từ As đến Co (1 – 10)
• Danh mục và lịch sử các đường cong/Phần 2. Từ Co đến Eq (11 – 21)
• Danh mục và lịch sử các đường cong/Phần 3. Từ Fe đến Ka (22 – 32)
• Danh mục và lịch sử các đường cong/Phần 4. Từ Ka đến Pa (33 – 42)
• Danh mục và lịch sử các đường cong/Phần 5. Từ Pe đến Rh (43 – 48)
• Danh mục và lịch sử các đường cong/Phần 6. Từ Ri đến Sp (49 – 53)
• Danh mục và lịch sử các đường cong/Phần 7. Từ Sp đến Tr (54 – 58)