Danh mục và lịch sử các đường cong/Phần 6. Từ Ri đến Sp (49 – 53)
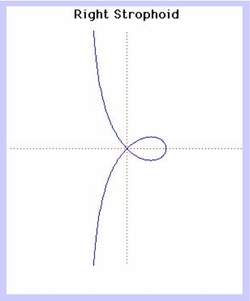
49. Right strophoid (Đường strophoid vuông)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
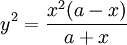
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
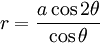
Đường strophoid đầu tiên xuất hiện trong công trình của Isaac Barrow vào năm 1670.
Tuy nhiên Torricelli đã từng mô tả đường cong này trong những văn bản của ông khoảng năm 1645 và Roberval tìm thấy nó như một quỹ tích của tiêu điểm của hình conic thu được khi mặt phẳng cắt hình nón quay quanh tiếp tuyến tại đỉnh của nó.
Tên
gọi
strophoid
vuông
này
được
đề
xuất
bởi
Montucci
vào
năm
1846.
Các
strophoid
tổng
quát
có
phương
trình
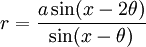 .
.
Các
trường
hợp
đặc
biệt
của
một
strophoid
vuông
khi
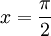 và
phương
trình
trong
hệ
cartesians
và
tọa
độ
cực,
đã
được
đưa
ra
như
trên.
và
phương
trình
trong
hệ
cartesians
và
tọa
độ
cực,
đã
được
đưa
ra
như
trên.
Diện
tích
của
vòng
lặp
của
strophoid
vuông
và
diện
tích
giữa
đường
cong
và
tiệm
cận
của
nó
cùng
bằng
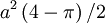
Gọi (C) là đường tròn có tâm tại điểm nơi strophoid vuông đi qua trục x, và bán kính là khoảng cách từ điểm đó đến gốc tọa độ. Khi đó strophoid là bất biến đối với phép đảo ngược trong đường tròn (C). Do đó có thể xem strophoid là một đường cong trong họ anallagmatic.
50. Serpentine Curve (Đường uốn khúc serpentine)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
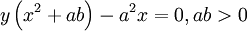
Đường cong uốn khúc serpentine đã được de L'Hôpital và Huygens nghiên cứu trước đó vào năm 1692.
Tuy nhiên nó được đặt tên và nghiên cứu chính thức bởi Newton vào năm 1701.
Đường cong này thuộc lớp phân loại các đường bậc 3 được viết trong cuốn Curves (Các đường cong) của Sir Isaac Newton trong Tuyển tập Lexicon Technicum (Tự điển kỹ thuật), Nhà xuất bản John Harris in tại London năm 1710.
Newton
chỉ
ra
rằng
các
đường
cong
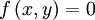 ,
trong
đó
,
trong
đó
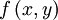 là
hàm
bậc
3,
có
thể
được
chia
thành
một
trong
bốn
dạng
chuẩn.
Dạng
đầu
tiên
trong
số
này
là
phương
trình
có
dạng
là
hàm
bậc
3,
có
thể
được
chia
thành
một
trong
bốn
dạng
chuẩn.
Dạng
đầu
tiên
trong
số
này
là
phương
trình
có
dạng
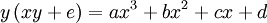
Đây là trường hợp khó khăn nhất trong việc phân loại, serpentine chỉ là một trong những trường hợp nhỏ thuộc phân lớp đầu tiên.
Guillaume
François
Antoine,
Marquis
de
l'Hôpital,
sinh
1661
tại
Paris
-
mất
ngày
02
tháng
2
năm
1704,
Paris
-
là
một
nhà
toán
học
Pháp.
Tên
của
ông
gắn
liền
với
quy
tắc
l'Hôpital's
để
tính
giới
hạn
liên
quan
đến
các
dạng
vô
định
 và
và
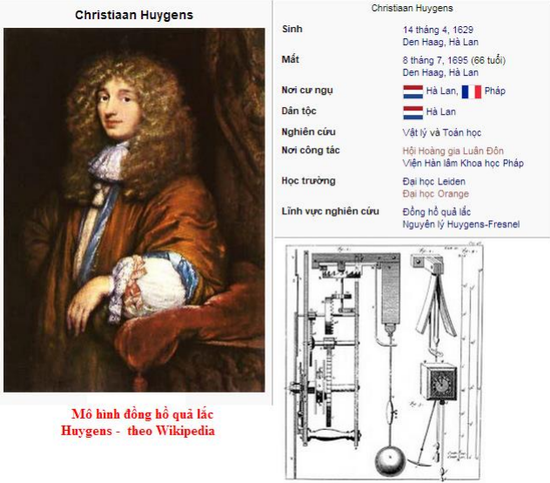
Christiaan Huygens, sinh 14 tháng 4 năm 1629 – mất 8 tháng 7 năm 1695 - là một nhà toán học, thiên văn học và vật lý học người Hà Lan. Ông được coi là một trong những nhà khoa học tiên phong của Cách mạng Khoa học với những nghiên cứu mang tính đột phá trong các lĩnh vực Toán học, Vật lý và Thiên văn học. Huygens còn là một nhà phát minh lớn đặc biệt với các sáng chế về đồng hồ.
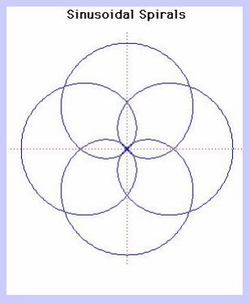
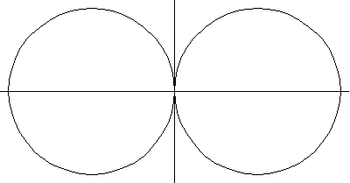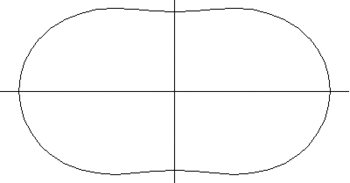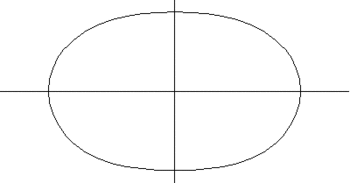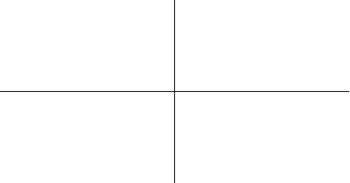
51. Sinusoidal Spirals (Đường xoắn ốc hình sin)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
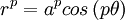
Đường xoắn ốc hình sin có thể chứa số p hữu tỷ bất kỳ trong công thức trên. Nhiều đường cong chuẩn xảy ra như đường xoắn ốc hình sin.
Nếu p = – 1, ta có phương trình đường thẳng.
Nếu p = 1 ta có phương trình đường tròn.
Nếu p = 1/2 ta có phương trình cardioid.
Nếu p = – 1 / 2 ta có phương trình parabola.
Nếu p = – 2 ta có phương trình hyperbola.
Nếu p = 2, ta có phương trình lemniscate của Bernoulli.
Đường xoắn ốc hình sin lần đầu tiên được nghiên cứu bởi Maclaurin.
Các
đường
xoắn
ốc
sin:
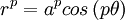 đảo
ngược
thành :
đảo
ngược
thành :
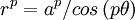 nếu
tâm
của
phép
nghịch
đảo
tại
điểm
cực.
nếu
tâm
của
phép
nghịch
đảo
tại
điểm
cực.
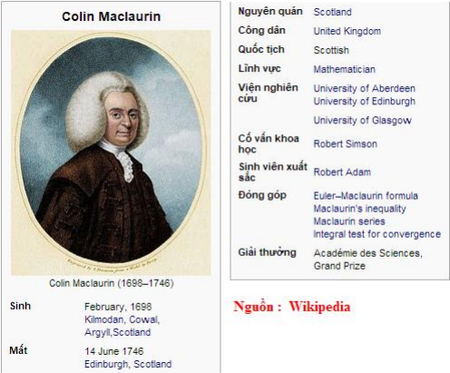
Colin Maclaurin (tháng 2 năm 1698 - ngày 14 tháng 6 1746) là một nhà toán học người Scotland đã có những đóng góp quan trọng vào hình học và đại số. Chuỗi Maclaurin, một trường hợp đặc biệt của chuỗi Taylor, đã được mang tên ông. Maclaurin sử dụng chuỗi Taylor để đặc trưng hóa cực đại, cực tiểu và các điểm uốn cho các hàm khả vi vô hạn trong tác phẩm " Treatise of Fluxions " của ông.
Maclaurin cũng đã có những đóng góp đáng kể về công trình nghiên cứu sức hấp dẫn của ellipsoids, một chủ đề đã từng thu hút sự chú ý của d'Alembert, A.-C. Clairaut, Euler, Laplace, Legendre, Poisson và Gauss. Maclaurin chỉ ra rằng hình spheroid dẹt là một trạng thái cân bằng khả dĩ trong lý thuyết hấp dẫn của Newton.
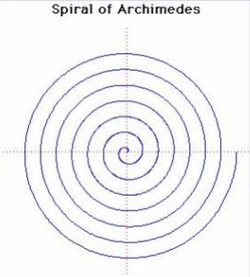
52. Spirals of Archimedes (Đường xoắn Archimedes)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
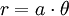
Đường xoắn ốc này được nghiên cứu bởi Archimedes trong khoảng 225 trước Công nguyên trong một tác phẩm " Về các đường xoắn ốc ". Sau đó Conon – một người bạn của ông - tiếp tục nghiên cứu.
Archimedes có lẽ đã tìm ra chiều dài của tiếp tuyến khác nhau của đường xoắn ốc. Nó có thể được sử dụng để chia góc làm 3 phần bằng nhau và bình phương đường tròn. Đường cong có thể được sử dụng như là một cam biến đổi chuyển động góc đều thành chuyển động tuyến tính đều.
Lấy
cực
như
là
tâm
của
phép
nghịch
đảo,
đường
xoắn
ốc
Archimedes
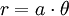 biến
đổi
thành
đường
xoắn
ốc
hyperbolic
biến
đổi
thành
đường
xoắn
ốc
hyperbolic
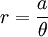 .
.
Archimedes là nhà toán học nổi tiếng nhất của thời cổ đại. Đóng góp của ông trong hình học đã cách mạng hóa đối tượng và phương pháp tư duy của ông dự đoán phép tính tích phân trước Newton và Leibniz đến 2.000 năm. Archimedes là một con người hoàn toàn thực tế, ông đã phát minh ra một loạt các máy bao gồm các ròng rọc và vít cũng như thiết bị bơm Archimidean.
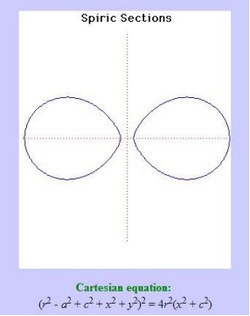
53. Spiric Section (Đường tiết diện xoắn)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
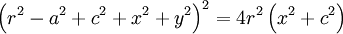
Sau khi Menaechmus xây dựng tiết diện conic bằng cách cắt một hình nón bởi một mặt phẳng, 200 năm sau đó - khoảng 150 trước Công nguyên -, nhà toán học Hy Lạp Perseus tiếp tục nghiên cứu các đường cong thu được bằng cách cắt một hình xuyến bởi một mặt phẳng song song với đường thẳng đi qua các tâm của lỗ xuyến. Các đường này có tên là đường tiết diện xoắn - spiric sections.
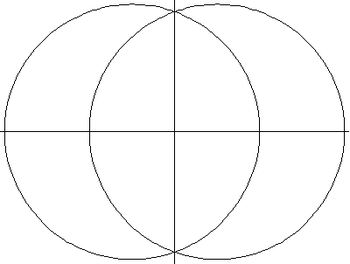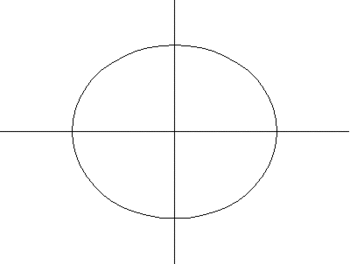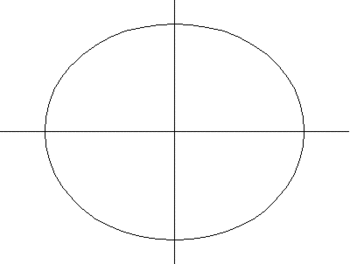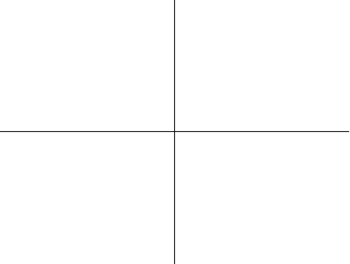
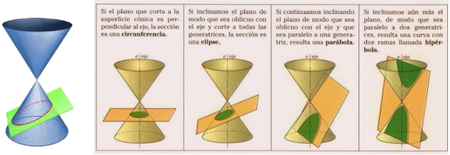
Hình minh họa tiết diện xoắn
Trong công thức của đường cong được đưa ra trên đây, hình xuyến được hình thành từ một đường tròn bán kính là a có tâm quay theo một đường tròn bán kính r. Giá trị của c cho ta khoảng cách của mặt phẳng cắt tính từ tâm của hình xuyến.
Khi c = 0 đường cong gồm hai đường tròn có bán kính là a, có tâm tại I(r, 0) và J(-r, 0).
Nếu c = r + a, đường cong gồm một điểm, thường gọi là gốc, trong khi nếu c > r + a, thì không có một điểm nào nằm trên đường cong.
Menaechmus, (sinh 380 BC, tại Alopeconnesus, Tiểu Á tại Thổ Nhĩ Kỳ- mất 320 BC,. Cyzicus (hiện nay là Kapidaği Yarimadasi, Thổ Nhĩ Kỳ), nhà toán học Hy Lạp và người bạn của Plato là người đã phát hiện ra tiết diện hình nón và mặt phẳng.
Menaechmus được cho là đã từng làm gia sư của Alexander Đại đế, niềm tin này bắt nguồn từ giai thoại sau đây: Một lần, khi Alexander hỏi Menaechmus cho một tóm tắt về phương pháp học tập và nghiên cứu về hình học, ông trả lời: "Tâu bệ hạ, để đi du lịch trên toàn quốc, có đường bộ dành cho hoàng gia và cũng có những con đường cho thứ dân, nhưng trong hình học chỉ có một con đường dành cho tất cả "(Beckmann 1989, trang 34.). Tuy nhiên, giai thoại này lần đầu tiên cũng được cho là của Stobaeus AD 500 ~, vì vậy việc Menaechmus có thực sự dạy Alexander là điều không chắc chắn.
Việc cho rằng Menaechmus phát hiện ra rằng hình elip, parabola, và hyperbola là các tiết diện của một hình nón và một mặt phẳng cho trước có nguồn gốc từ một đoạn thơ của Eratosthenes xứ Cyrene (c. 276-194 bc) trong đó đề cập việc cắt hình nón "theo bộ ba của Menaechmus." Eutocius xứ Ascalon (ad 520) đã thuật lại hai trong số các lời giải của Menaechmus cho bài toán dựng một khối lập phương với thể tích gấp đôi một khối lập phương khác có cạnh bằng a. Lời giải của Menaechmus sử dụng tính chất của parabol và hyperbola để tạo ra những đoạn thẳng x và y thỏa mãn tỷ lệ thức sau: a: x = x: y = y: 2a
Có một văn bản của Plutarch thuật lại rằng Plato đã không chấp thuận phương pháp giải quyết bài toán gấp đôi khối lập phương của Menaechmus bằng việc sử dụng các thiết bị cơ học; việc chứng minh cho bài toán này hiện nay đang được biết đến là phương pháp thuần đại số.
Menaechmus mất năm 320 BC. Nơi ông qua đời chính xác ở đâu cũng là điều không chắc chắn, mặc dù nhiều học giả hiện đại cho rằng ông cuối cùng đã mất tại Cyzicus.
Perseus (c. 150 trước Công nguyên) là nhà hình học Hy Lạp cổ đại, người phát minh ra khái niệm về tiết diện xoắn spiric sections, tương tự tiết diện conic đã được Apollonius xứ Perga nghiên cứu.
Các chi tiết về cuộc đời của Perseus rất ít được biết đến, chỉ được đề cập qua loa từ Proclus và Geminus và những công trình nghiên cứu của ông thì hầu như bị mai một.
Đường tiết diện xoắn Spiric sections là một trường hợp đặc biệt của một tiết diện toric, và là một trong các tiết diện toric đầu tiên được mô tả.
Spiric sections nổi tiếng nhất là hình bầu dục Cassini, đó là quỹ tích của các điểm có tích 2 khoảng cách từ điểm đó đến hai tiêu điểm là một hằng số.
Để so sánh, một hình elip có tổng 2 khoảng cách từ điểm đó đến hai tiêu điểm là một hằng số, hyperbola có hiệu 2 khoảng cách từ điểm đó đến hai tiêu điểm là một hằng số; và đường tròn có một tỉ lệ không đổi giữa 2 khoảng cách tiêu điểm.
Bằng định nghĩa tâm sai, ta có
- Tâm sai của đường tròn là không: e = 0.
- Tâm sai của elip - lớn hơn 0 nhưng nhỏ hơn 1; 0 < e < 1
- Tâm sai của parabola là 1; e = 1
- Tâm sai của hyperbola lớn hơn 1; e > 1
| conic section | equation | eccentricity (e) | linear eccentricity (c) |
|---|---|---|---|
| circle |
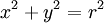 |
0 | 0 |
| ellipse |
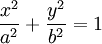 |
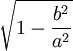 |
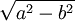 |
| parabola |
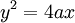 |
1 | a |
| hypebola |
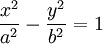 |
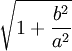 |
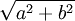 |
Tham khảo[sửa]
1. http://www-history.mcs.st-andrews.ac.uk/Curves/Curves.html
2. http://www-history.mcs.st-andrews.ac.uk/
3. Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers. Department of Mathematics, Computer Science, and Statistics,Bloomsburg University Bloomsburg, Pennsylvania 17815.
4. A Handbook on curves and their properties. Robert C. Yates, printed by Edwards Brothers, Inc - Ann Arbor, Michigan U.S.A.
Bản quyền[sửa]
Biên tập và trích dịch.
Ngày 01/04/2012
Mục lục[sửa]
- Giới thiệu
- Phần 1. Từ As đến Co (1 – 10)
- Phần 2. Từ Co đến Eq (11 – 21)
- Phần 3. Từ Fe đến Ka (22 – 32)
- Phần 4. Từ Ka đến Pa (33 – 42)
- Phần 5. Từ Pe đến Rh (43 – 48)
- Phần 6. Từ Ri đến Sp (49 – 53)
- Phần 7. Từ Sp đến Tr (54 – 58)
- Phần 8. Từ Tr đến Wi (59 – 63)
Bài liên quan
Liên kết đến đây
- Danh mục và lịch sử các đường cong
- Bản mẫu:Danh mục và lịch sử các đường cong
- Danh mục và lịch sử các đường cong/Phần 1. Từ As đến Co (1 – 10)
- Danh mục và lịch sử các đường cong/Phần 2. Từ Co đến Eq (11 – 21)
- Danh mục và lịch sử các đường cong/Phần 3. Từ Fe đến Ka (22 – 32)
- Danh mục và lịch sử các đường cong/Phần 4. Từ Ka đến Pa (33 – 42)
- Danh mục và lịch sử các đường cong/Phần 5. Từ Pe đến Rh (43 – 48)
- Danh mục và lịch sử các đường cong/Phần 7. Từ Sp đến Tr (54 – 58)
- Danh mục và lịch sử các đường cong/Phần 8. Từ Tr đến Wi (59 – 63)