Danh mục và lịch sử các đường cong/Phần 3. Từ Fe đến Ka (22 – 32)
Mục lục
- 1 22. Fermat’s Spiral (Đường xoắn ốc Fermat)
- 2 23. Folium (Đường hình lá)
- 3 24. Folium of Descartes (Đường hình lá Descartes)
- 4 25. Freeth’s Nephroid (Đường cong Nephroid Freeths)
- 5 26. Frequency Curve (Đường cong tần số)
- 6 27. Hyperbola (Đường cong Hyperbole)
- 7 28. Hyperbolic Spiral (Đường xoắn ốc Hyperbolic)
- 8 29. Hypocycloid (Đường cong Hypocycloid)
- 9 30. Hypotrochoid (Đường cong Hypotrochoid)
- 10 31. Involute of a Circle (Đường pháp bao trong của đường tròn)
- 11 32. Kampyle Eudoxus (Đường cong Kampyle Eudoxus)
- 12 Tham khảo
- 13 Bản quyền
- 14 Mục lục
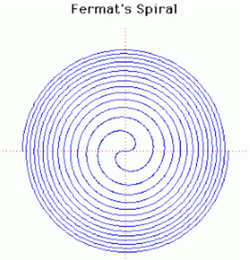
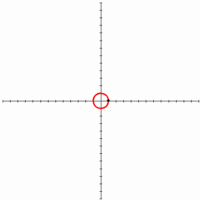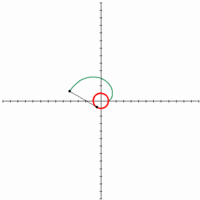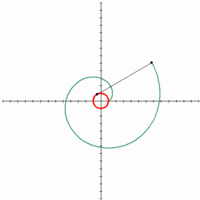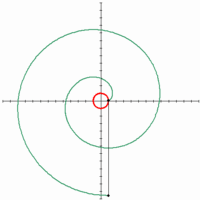
22. Fermat’s Spiral (Đường xoắn ốc Fermat)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
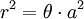
Đường xoắn ốc này đã được Fermat tìm ra năm 1636.
Đối với bất kỳ giá trị θ dương, hàm có hai giá trị tương ứng của r, một có giá trị dương và một mang những giá trị âm có cùng trị tuyệt đối. Do đó các đường xoắn ốc sẽ đối xứng qua đường phân giác thứ hai y = – x như có thể thấy từ những đường cong hiển thị ở trên.
Đường
nghịch
đảo
của
Spiral
Fermat,
khi
chọn
cực
là
tâm
nghịch
đảo
cũng
là
một
đường
xoắn
ốc
có
phương
trình
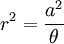
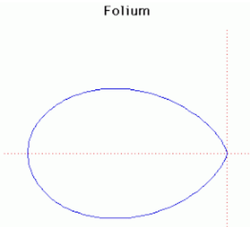
23. Folium (Đường hình lá)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
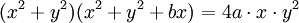
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
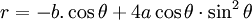
Dạng
tổng
quát
của
folium
được
cho
bởi
công
thức
trên.
Folium
có
nghĩa
là
hình
lá.
Có
ba
dạng
đặc
biệt
của
folium:
folium
đơn,
folium
đôi
và
folium
ba.
tương
ứng
với
các
trường
hợp
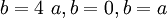 Các
biểu
đồ
được
vẽ
ở
trên
là
folium
đơn
giản.
Các
biểu
đồ
được
vẽ
ở
trên
là
folium
đơn
giản.
24. Folium of Descartes (Đường hình lá Descartes)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
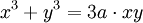
Phương
trình
tham
số
đường
cong
trong
hệ
tọa
độ
Descartes:
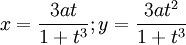
Đường hình lá này đầu tiên được Descartes đề cập đến vào năm 1638, ông đã tìm thấy hình dạng chính xác của đường cong ở phần tư thứ nhất góc tọa độ, nhưng ông lại cho rằng hình dạng lá này được lặp đi lặp lại trong mỗi phần tư góc toạ độ còn lại như cánh của bông hoa. Đồ thị đường cong này đối xứng qua phân giác thứ nhất y = x. Bài toán xác định các tiếp tuyến với đường cong đã được đề xuất bởi Roberval, là người cũng sai khi tin rằng đường cong có dạng một bông hoa nhài. (tên gọi Fleur de jasmin - sau đó đã được thay đổi). Đường cong này đôi khi được gọi là đường de noeud ruban. Khi Fermat phát hiện ra phương pháp tìm tiếp tuyến, Descartes đã thách thức Fermat viết phương trình tiếp tuyến với đường cong này tại một điểm tùy ý. Fermat giải quyết bài toán này rất dễ dàng, và đó là điều mà Descartes đã không thể giải được.
Folium
có
một
đường
tiệm
cận
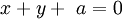 .
.
Các
phương
trình
tiếp
tuyến
tại
điểm
t
=
p
là
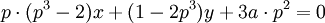
Đường
cong
đi
qua
gốc
O
lần
thứ
nhất
tại
t
=
0
và
tiến
về
gốc
O
lần
thứ
hai
khi
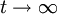
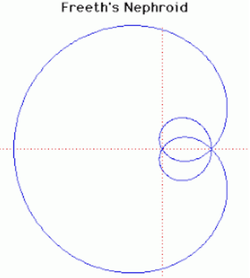
25. Freeth’s Nephroid (Đường cong Nephroid Freeths)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
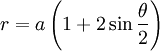
Đây là đường cong strophoid của một đường tròn với cực O là tâm và điểm P cố định trên chu vi của đường tròn.Trong hình ở trên, O là gốc và P là nút nơi đường cong đi qua ba lần.
Nếu
đường
thẳng
qua
P
song
song
với
trục
y
cắt
nephroid
tại
A
khi
đó
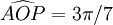 Điều
này
có
thể
được
sử
dụng
để
dựng
một
đa
giác
đều
7
cạnh.
T.J.
Freeths
(1819-1904)
là
một
nhà
toán
học
Anh.
Trong
bài
báo
được
xuất
bản
bởi
Hội
Toán
học
London
vào
năm
1879
ông
đã
mô
tả
đặc
điểm
của
những
strophoids
khác
nhau,
bao
gồm
cả
strophoid
trisectrix.
Điều
này
có
thể
được
sử
dụng
để
dựng
một
đa
giác
đều
7
cạnh.
T.J.
Freeths
(1819-1904)
là
một
nhà
toán
học
Anh.
Trong
bài
báo
được
xuất
bản
bởi
Hội
Toán
học
London
vào
năm
1879
ông
đã
mô
tả
đặc
điểm
của
những
strophoids
khác
nhau,
bao
gồm
cả
strophoid
trisectrix.
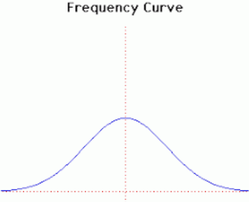
26. Frequency Curve (Đường cong tần số)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
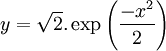
Đường cong này còn được gọi đường cong sai số chuẩn tắc, do nhà toán học de Moivre phát hiện ra năm 1733. Nó cũng đã được Laplace và Gauss nghiên cứu về nhiều lĩnh vực.Tên gọi đường cong tần số cũng được áp dụng cho một loạt các đường cong khác.
Vài nét về các nhà toán học có công nghiên cứu về đường cong tần số:
+ De Moivre là nhà toán học Pháp, người tiên phong trong lĩnh vực hình học giải tích và lý thuyết xác suất.
+ Carl Friedrich Gauss, nhà bác học Đức, đã có rất nhiều công trình đóng góp cả về toán và vật lý. Có thể kể như lý thuyết số, giải tích, hình học vi phân, lý thuyết đo đạc, từ tính học, thiên văn học và quang học. Những công trình của Carl Friedrich Gauss đã có ảnh hưởng rất sâu sắc trong nhiều lĩnh vực khác nhau.
+ Pierre-Simon Laplace đã chứng minh tính ổn định của thái dương hệ. Trong lĩnh vực giải tích ông đã giới thiệu hàm thế và các hệ số Laplace. Ông cũng là người đặt nền tảng cho lý thuyết xác suất toán học.
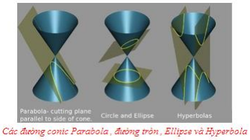
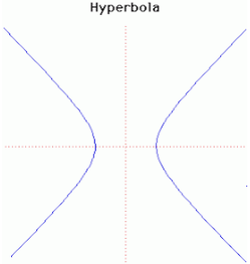
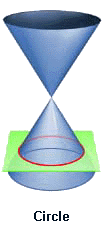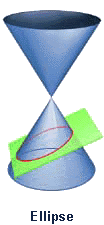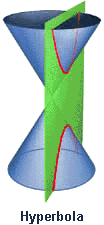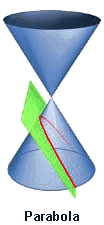
27. Hyperbola (Đường cong Hyperbole)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
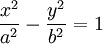
Phương
trình
tham
số
trong
hệ
tọa
độ
Descartes:
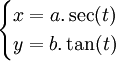
Một
trường
hợp
đặc
biệt
của
hyperbola
lần
đầu
tiên
được
nghiên
cứu
bởi
Menaechmus.
Trường
hợp
đặc
biệt
này
hyperbola
có
2
tiệm
cận
vuông
góc
và
phương
trình
của
nó
là
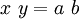 (còn
được
gọi
là
một
hyperbola
hình
chữ
nhật)
(còn
được
gọi
là
một
hyperbola
hình
chữ
nhật)
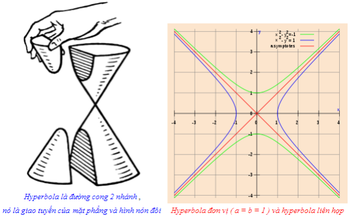
Euclid và Aristaeus viết về các hyperbola tổng quát nhưng chỉ tập trung nghiên cứu một nhánh của nó, trong khi các hyperbola có được tên gọi hiện nay là do Apollonius, người đầu tiên nghiên cứu hai nhánh của hyperbola. Pappus cũng khảo sát tiêu điểm và đường chuẩn của một hyperbola.
Đường pháp bao ngoài của hyperbola với phương trình ở trên là đường cong Lame:
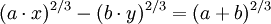
+ Apollonius of Perga được biết đến như một " nhà hình học vĩ đại ". Có rất ít tư liệu về cuộc sống của ông, nhưng các công trình của Apollonius đã ảnh hưởng rất lớn về sự phát triển của toán học - đặc biệt nhất là cuốn sách nổi tiếng Conics, đã giới thiệu các khái niệm rất quen thuộc với chúng ta ngày nay như parabola, hyperbola và ellipse.
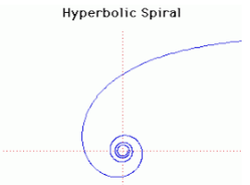
28. Hyperbolic Spiral (Đường xoắn ốc Hyperbolic)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
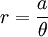
Đường xoắn ốc hyperbolic có nguồn gốc với Pierre Varignon vào năm 1704. Nó được Johann Bernoulli nghiên cứu từ năm 1710 và 1713 và Cotes năm 1722. Đường Roulette của cực đường xoắn ốc hyperbolic lăn không trượt trên một đường thẳng là một tractrix. Pierre Varignon (1654-1722) là giáo sư toán học tại Collège Mazarin và sau đó là tại Collège Hoàng gia. Con đường đưa Pierre Varignon đến toán học là khi ông đọc tác phẩm Euclid, ông cũng đọc Géométrie Descartes ', và sau đó ông quyết định cống hiến sự nghiệp mình cho khoa học và toán học. Ông là một trong những học giả người Pháp đầu tiên nhận ra giá trị của bộ môn giải tích. Những đóng góp chính của ông là trong lĩnh vực cơ học.
Nếu
điểm
cực
là
tâm
của
phép
nghịch
đảo,
thì
đường
xoắn
ốc
hyperbolic
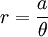 đảo
ngược
thành
đường
xoắn
ốc
Archimedes
đảo
ngược
thành
đường
xoắn
ốc
Archimedes
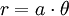 .
.
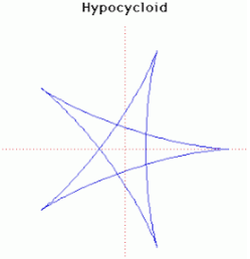
29. Hypocycloid (Đường cong Hypocycloid)[sửa]
Phương trình tham số trong hệ tọa độ Descartes:
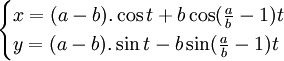
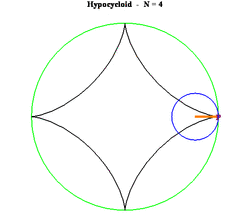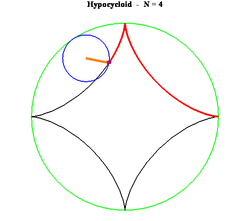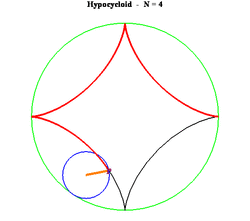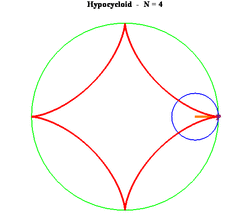
Có bốn đường cong liên quan chặt chẽ với nhau. Đó là epicycloid, epitrochoid, hypocycloid và hypotrochoid và đều được vẽ từ một điểm P trên một đường tròn bán kính b lăn không trượt trên một đường tròn bán kính cố định a. Đối với hypocycloid, là một ví dụ trong số đó được hiển thị ở trên, đường tròn bán kính b cuộn vào bên trong vòng tròn bán kính a. P là điểm trên chu vi của vòng tròn bán kính b. Đối với ví dụ trên đây ta có a = 5 và b = 3.(a > b)
Những đường cong này đã được nghiên cứu bởi Dürer (1525), Desargues (1640), Huygens (1679), Leibniz, Newton (1686), de L'Hôpital (năm 1690), Jacob Bernoulli (1690), la Hire (1694), Johann Bernoulli (1695), Daniel Bernoulli (1725), Euler (1745, 1781).
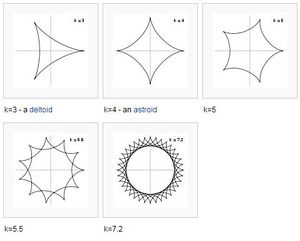
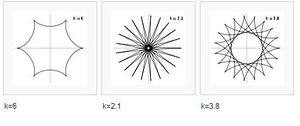
Trường hợp đặc biệt là 3b = a khi đó ta thu được tricuspoid và khi 4b = a ta có đường astroid.
Đặt k = a / b khi đó đồ thị hypocycloid có dạng
Dưới đây là một trình Java minh họa Epicycloid và Hypocycloid. Di chuyển các thanh màu vang, tím, xanh và xanh cây để xem đồ thị các đường cong tương ứng.
Mã nhúng:
<br /> <iframe align="MIDDLE" frameborder="0" height="590" src="http://www.carloslabs.com/projects/200805B/index.html" width="370"></iframe> <br />
Nguồn: http://www.carloslabs.com/projects/200805B/index.html
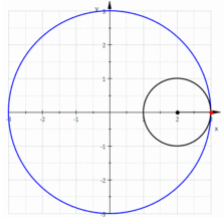
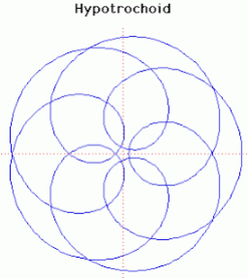
30. Hypotrochoid (Đường cong Hypotrochoid)[sửa]
Phương trình tham số trong hệ tọa độ Descartes:
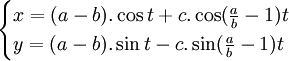
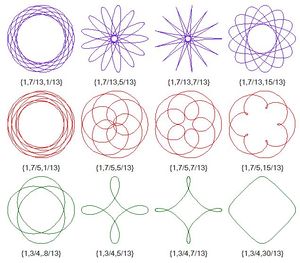
Những đường cong này được nghiên cứu bởi La Hire, Desargues, Leibniz, Newton và nhiều người khác.
Có bốn đường cong liên quan chặt chẽ với nhau. Đó là epicycloid, epitrochoid, hypocycloid và hypotrochoid và đều được vẽ từ một điểm P trên một vòng tròn bán kính b cuộn quanh một vòng tròn bán kính a cố định.
Đối với hypotrochoid, là một ví dụ trong số đó được hiển thị ở trên, vòng tròn bán kính b cuộn vào bên trong vòng tròn bán kính a. P là điểm có khoảng cách c tính từ tâm của vòng tròn bán kính b. Trong ví dụ này a = 5, b = 7 và c = 2,2. Một số đồ thị và clip mô tả chuyển động hypotrochoid.
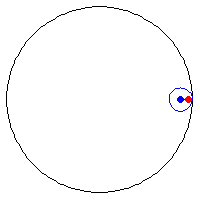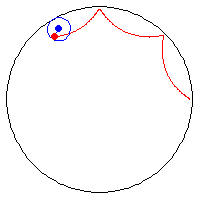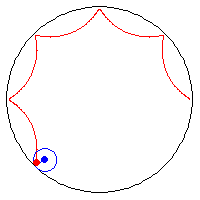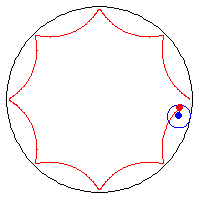
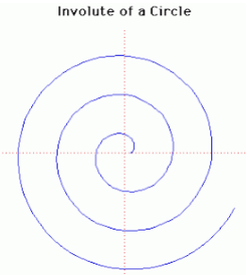
31. Involute of a Circle (Đường pháp bao trong của đường tròn)[sửa]
Phương trình tham số trong hệ tọa độ Descartes:
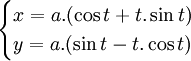
Đường pháp bao trong của một đường tròn là quỹ tích tạo ra bởi một điểm trên một đường thẳng cuộn xung quanh một vòng tròn. Huygens đã nghiên cứu đường cong này khi ông cố gắng tìm những chiếc đồng hồ không có quả lắc có thể dùng được trên tàu biển. Ông đã vận dụng tính chất đường pháp bao trong của đường tròn cho đồng hồ quả lắc với nỗ lực cưỡng bức con lắc chuyển động theo quỹ đạo của một cycloid.
Phát minh ra một chiếc đồng hồ giữ thời gian chính xác trên biển là một vấn đề lớn và việc tìm một giải pháp đã được đặt ra trong nhiều năm. Vấn đề này có tầm quan trọng sống còn vì nếu biết được giờ GMT thì sau đó, giờ địa phương và kinh độ có thể dễ dàng tính được từ mặt trời.
Ứng dụng: Leonhard Euler đề xuất sử dụng đường pháp bao trong của đường tròn cho hình dạng răng cưa của bánh răng toothwheel, một trong những ứng dụng phổ biến hiện nay, được gọi là bánh răng trong.
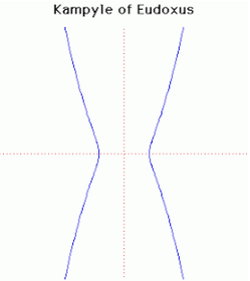
32. Kampyle Eudoxus (Đường cong Kampyle Eudoxus)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
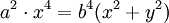
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
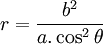
Đây là đường cong được nghiên cứu bởi Eudoxus liên quan đến bài toán cổ điển về nhân đôi khối lập phương.
Eudoxus là một học trò của Plato. Công trình chính của ông là trong lĩnh vực thiên văn học. Ông là người đầu tiên mô tả các chòm sao và đã phát minh ra thiên văn kế. Ông cũng giới thiệu các đề tài nghiên cứu về thiên văn-toán học vào Hy Lạp.
Eudoxus tìm thấy công thức để đo kim tự tháp hình nón và hình trụ. Tác phẩm của ông chứa các cơ sờ về tính toán cùng với nhiều nghiên cứu rất chặt chẽ về phương pháp khử (vét cạn).
Chú thích: - Không nên nhầm lẫn với Eudoxus Cyzicus
Tham khảo[sửa]
1. http://www-history.mcs.st-andrews.ac.uk/Curves/Curves.html
2. http://www-history.mcs.st-andrews.ac.uk/
3. Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers. Department of Mathematics, Computer Science, and Statistics, Bloomsburg University Bloomsburg, Pennsylvania 17815.
4. A Handbook on curves and their properties. Robert C. Yates, printed by Edwards Brothers, Inc - Ann Arbor, Michigan U.S.A.
Bản quyền[sửa]
Biên tập và trích dịch.
Ngày 01/04/2012
Mục lục[sửa]
- Giới thiệu
- Phần 1. Từ As đến Co (1 – 10)
- Phần 2. Từ Co đến Eq (11 – 21)
- Phần 3. Từ Fe đến Ka (22 – 32)
- Phần 4. Từ Ka đến Pa (33 – 42)
- Phần 5. Từ Pe đến Rh (43 – 48)
- Phần 6. Từ Ri đến Sp (49 – 53)
- Phần 7. Từ Sp đến Tr (54 – 58)
- Phần 8. Từ Tr đến Wi (59 – 63)
Bài liên quan
Liên kết đến đây
- Danh mục và lịch sử các đường cong
- Bản mẫu:Danh mục và lịch sử các đường cong
- Danh mục và lịch sử các đường cong/Phần 1. Từ As đến Co (1 – 10)
- Danh mục và lịch sử các đường cong/Phần 2. Từ Co đến Eq (11 – 21)
- Danh mục và lịch sử các đường cong/Phần 4. Từ Ka đến Pa (33 – 42)
- Danh mục và lịch sử các đường cong/Phần 5. Từ Pe đến Rh (43 – 48)
- Danh mục và lịch sử các đường cong/Phần 6. Từ Ri đến Sp (49 – 53)
- Danh mục và lịch sử các đường cong/Phần 7. Từ Sp đến Tr (54 – 58)
- Danh mục và lịch sử các đường cong/Phần 8. Từ Tr đến Wi (59 – 63)