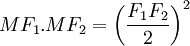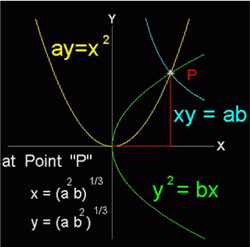Danh mục và lịch sử các đường cong/Phần 4. Từ Ka đến Pa (33 – 42)
Mục lục
- 1 33. Kappa Curve (Đường cong Kappa)
- 2 34. Lamé Curve (Đường cong Lamé)
- 3 35. Lemniscate of Bernoulli (Đường cong Lemniscate Bernoulli)
- 4 36. Limacon of Pascal (Đường hình ốc Limacon Pascal)
- 5 37. Lissajous Curve (Đường cong Lissajous)
- 6 38. Lituus Curve (Đường cong Lituus)
- 7 39. Neile‘s Semi-Cubical Parabola (Đường Parabola nửa-bậc-3 Neile)
- 8 40. Nephroid (Đường cong Nephroid)
- 9 41. Newton’s Diverging Parabolas (Đường parabola phân kỳ Newton)
- 10 42. Parabola (Đường parabola)
- 11 Tham khảo
- 12 Bản quyền
- 13 Mục lục
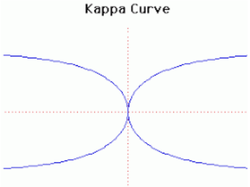
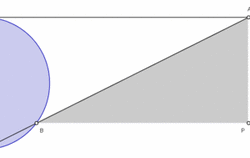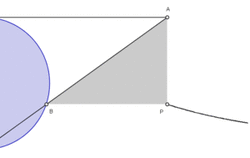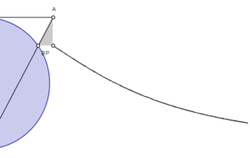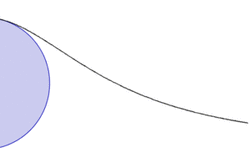
33. Kappa Curve (Đường cong Kappa)[sửa]
Phương trình đường cong trong hệ tọa độ Descartes:
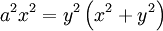
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
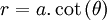
Các đường cong kappa cũng gọi là đường cong Gutschoven. Lần đầu tiên được nghiên cứu bởi G. Van Gutschoven khoảng 1662. Các đường cong này cũng được Newton nghiên cứu và một số năm sau đó bởi Johann Bernoulli.
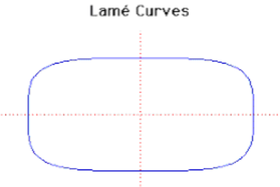
34. Lamé Curve (Đường cong Lamé)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
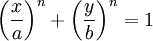
Năm 1818, Lame thảo luận về các đường cong này với phương trình ở trên. Ông khảo sát các đường cong tổng quát hơn với n là số nguyên. Nếu n là hữu tỷ thì đường cong có tính đại số, nhưng n vô tỷ thì đường cong có tính siêu việt.
-
Các
đường
cong
được
vẽ
ở
trên
là
trường
hợp
n
=
4.
Đối
với
số
mũ
nguyên
n
đường
cong
tiệm
cận
với
một
hình
chữ
nhật
khi
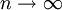 .
.
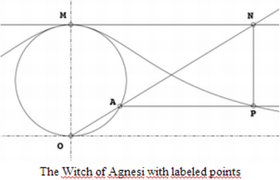
- Các trường hợp đặc biệt khi n = 2/3 đường cong là Astroid, khi n = 3 ta có đường cong thường được gọi là đường phù thuỷ Agnesi.
- Các trường hợp n = 5/2 dường cong có tên gọi là (siêu ellipse) superellipse _ liên quan đến kiến trúc sư - nhà thơ Piet Hein người Đan Mạch (ông cũng là nhà phát minh của khối vuông Soma) _đã được sử dụng cho nhiều mục đích, kể cả trong tính toán cầu, đường cao tốc và các ứng dụng kiến trúc khác.
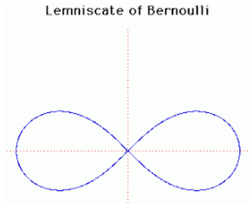
35. Lemniscate of Bernoulli (Đường cong Lemniscate Bernoulli)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
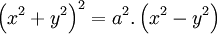
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
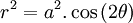
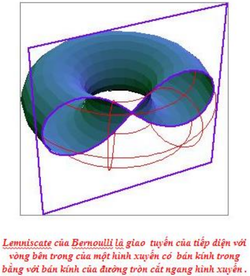
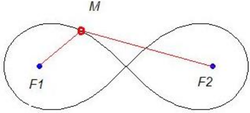
Năm 1694, Jacob Bernoulli cho đăng một bài viết trong Acta Eruditorumon nói về một đường cong có hình dạng giống như số 8 (hình một nút, hoặc cái nơ của một ruy băng) mà ông gọi là lemniscus xuất phát từ tiếng Latin (một mặt dây ruy băng ').
Jacob
Bernoulli
đã
không
nhận
thức
rằng
đường
cong
được
mô
tả
này
chỉ
là
một
trường
hợp
đặc
biệt
của
một
đường
Oval
Cassinian
đã
được
Cassini
mô
tả
vào
năm
1680.
Các
tính
chất
chung
của
lemniscate
được
phát
hiện
bởi
của
Giovanni
Fagnano
vào
năm
1750.
Các
công
trình
khảo
sát
của
Euler
về
độ
dài
của
vòng
cung
của
đường
cong
(1751)
sau
này
đã
dẫn
đến
việc
nghiên
cứu
các
hàm
số
elliptic.
Phương
trình
lưỡng
cực
của
lemniscate
có
dạng
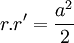
+ Giulio Fagnano Toschi, sinh tại Sinigaglia ngày 6 tháng 12 năm 1682, thuộc một gia đình quý tộc Marche là nhà toán học nổi tiếng với các thành tựu về bộ môn hình học.
Ông đã hoàn thành nghiên cứu đầu tiên tại trường Cao đẳng Clementine thành phố Rome. Mặc dù tự học toán, nhưng ông đã đạt được tầm cỡ quốc tế, nổi tiếng nhờ những đóng góp đáng kể về nhiều chủ đề khác nhau. Ông là người đề xuất phương pháp mới giải các phương trình II, III và IV và phát hiện ra công thức để tính toán trọng tâm tam giác. Trong số các nghiên cứu của ông về lemniscate, Fagnano giới thiệu các phép biến đổi giải tích từ đó đã có những đóng góp vào việc phát triển các hàm elliptic. Năm 1750 ông viết hai tuyển tập kết quả các công trình nghiên cứu có tựa đề "Sản xuất toán học" (Production Mathematics). Trong đó quan trọng nhất là những nghiên cứu về tổ hợp, đặc biệt về xổ số.
Giulio Fagnano rất có công trong việc hỗ trợ cho một số nhà toán học trẻ đương thời, trong đó có Joseph Lagrange. Ông có 12 người con, John con ông, cũng là người đã theo bước chân của cha mình trong các lĩnh vực Toán học. Ông là thành viên của Hội Hoàng gia London và Viện Hàn lâm Khoa học Berlin. Fagnano mất tại thành phố quê hương của mình ngày 26 tháng 9 năm 1766 trước khi được bầu vào Académie des Sciences ở Paris.
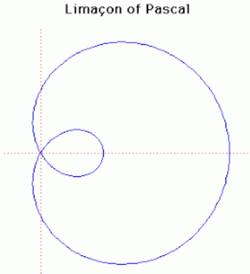
36. Limacon of Pascal (Đường hình ốc Limacon Pascal)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
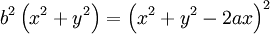
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
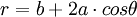
Limacon là đường cong thuộc họ anallagmatic.Đường cong Limacon Pascal được Étienne Pascal (cha của Blaise Pascal) phát hiện và đặt tên bởi một người Pháp Gilles-Personne Roberval năm 1650. Étienne Pascal sử dụng đường cong này như là một ví dụ về phương pháp vẽ tiếp tuyến dựa vào vi phân.
Cái tên 'limacon' có nghĩa theo tiếng Latin là từ 'ốc'. Étienne Pascal đã từng trao đổi thư từ với Mersenne, là người đã tổ chức tư dinh thành một nơi gặp gỡ của các nhà hình học nổi tiếng bao gồm cả Roberval.
Thực ra Dürer mới chính là người phát hiện các đường cong trên khi ông đưa ra một phương pháp dựng hình, mặc dù ông không gọi nó là một limacon, trong tác phẩm Underweysung der Messung công bố năm 1525.
- Khi b = 2a ta có limacon biến đổi thành cardioid.
- Nếu b = a ta có dạng một trisectrix. Chú ý rằng trisectrix này không phải là Trisectrix của Maclaurin.
-
Nếu
b
≥
2a
thì
diện
tích
của
limacon
bằng
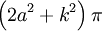
-
Nếu
b
=
a
(trường
hợp
được
vẽ
ở
trên
với
a
=
b
=
1)
thì
diện
tích
của
vòng
lặp
bên
trong
là
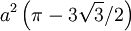 và
diện
tích
miền
giữa
các
vòng
là
và
diện
tích
miền
giữa
các
vòng
là
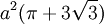
Một số clips về limacon với { a = 1, b = 1 }; { a = 1, b = 2 };{ a = 1, b = 3 };
Xem: Limacon Pascal 1 với { a = 1, b = 1 }
Xem: Limacon Pascal 2 với { a = 1, b = 2 }
Xem: Limacon Pascal 3 với { a = 1, b = 3 }
Xem chi tiết:
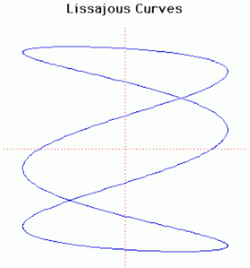
37. Lissajous Curve (Đường cong Lissajous)[sửa]
Phương
trình
tham
số
trong
hệ
tọa
độ
Descartes:
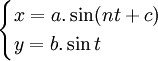
Đường cong Lissajous hoặc đồ thị Lissajous còn được gọi là đường cong Bowditch. Nathaniel Bowditch là người khảo sát chúng vào năm 1815. các đường cong này đã được Jules-Antoine Lissajous nghiên cứu một cách độc lập và chi tiết hơn vào năm 1857.
Các đường cong Lissajous có ứng dụng trong vật lý, thiên văn học và khoa học khác.
Nathaniel Bowditch (1773-1838) là người Mỹ. Ông đã học tiếng Latin để đọc tác phẩm Newton's Principia và sau đó tự học các ngôn ngữ khác để nghiên cứu toán học. Tác phẩm New Practical Navigator (1802) và bản dịch Mécanique Celeste Laplace của ông là một công trình nổi tiếng tầm cỡ quốc tế.
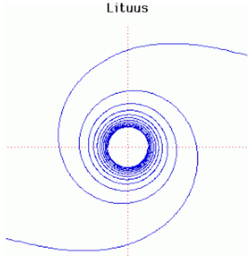
38. Lituus Curve (Đường cong Lituus)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
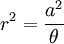
Các đường cong lituus nguồn gốc với tác giả Cotes năm 1722. Maclaurin sử dụng thuật ngữ này trong cuốn sách của ông tựa đề Harmonia Mensurarumin 1722. Lituus là quỹ tích của điểm P di chuyển sao cho diện tich của một cung tròn là một hằng số.
Roger Cotes (1682-1716) qua đời ở tuổi 34 ông đã xuất bản hai cuốn hồi ký trong đời của mình. Ông được bổ nhiệm giáo sư tại Cambridge ở tuổi 24 và các tác phẩm của ông được xuất bản sau khi ông mất. Cotes đã phát hiện ra một định lý quan trọng về căn bậc n của phần tử đơn vị, dự báo các phương pháp bình phương tối thiểu và phát hiện ra một phương pháp tích phân các hàm phân thức có mẫu số là nhị thức.
Roger Cotes cũng là người đã biên tập các ấn bản thứ hai tác phẩm Principia của Newton. Ông đã có những đóng góp tiến bộ trong lý thuyết về logarit, tích phân và phương pháp số, đặc biệt là nội suy.
Ông cũng phát minh ra công thức cầu phương được gọi là công thức Newton-Cotes và lần đầu tiên giới thiệu những chi tiết được biết đến sau này là công thức Euler. Ông cũng là Giáo sư Plumian đầu tiên tại Đại học Cambridge từ năm 1707 cho đến khi mất 1716. Xem chuyển động của vật thể trên đường cong Lituus, bắt đầu với r~2.
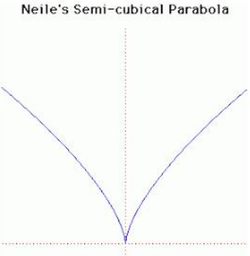
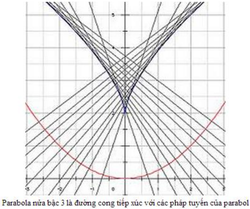
39. Neile‘s Semi-Cubical Parabola (Đường Parabola nửa-bậc-3 Neile)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
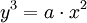
Đường cong này, đôi khi được gọi là parabol nửa bậc ba (bán lập phương), được William Neile phát hiện vào năm 1657. Đó là đường cong đại số đầu tiên mà chiều dài của nó đã được các nhà toán học nghiên cứu và tìm được. Wallis công bố phương pháp này vào năm 1659 cho đường cong Neile. Van Heuraet (người Hà Lan) cũng đã sử dụng các đường cong này cho các công trình tổng quát hơn.
William Neile sinh tại Bishopsthrope năm 1637. Ông là học trò của Wallis và đã tỏ ra có rất nhiều tiềm năng. Đường cong đại số parabol Neile là đường cong đại số đầu tiên mà các nhà toán học tính được chiều dài của nó, trước đó chỉ có chiều dài cung của các đường cong siêu việt như cycloid và đường xoắn ốc logarit là đã được tính toán. Thật không may, năm 1670 Neile qua đời lúc còn trẻ trước khi ông có thể còn đạt được nhiều thành tựu khác nữa.
Năm
1687
Leibniz
đặt
vấn
đề
đi
tìm
đường
cong
mô
tả
một
chất
điểm
rơi
xuống
dưới
tác
dụng
lực
hấp
dẫn
sao
cho
nó
có
thể
di
chuyển
những
khoảng
cách
thẳng
đứng
bằng
nhau
trong
một
khoảng
thời
gian
bằng
nhau.
Huygens
cho
thấy
rằng
parabol
bán
lập
phương
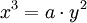 thoả
mãn
tính
chất
này.
Bởi
vì
đây
là
một
đường
cong
đẳng
thời.
Parabol
bán
lập
phương
là
đường
pháp
bao
ngoài
của
một
parabol.
thoả
mãn
tính
chất
này.
Bởi
vì
đây
là
một
đường
cong
đẳng
thời.
Parabol
bán
lập
phương
là
đường
pháp
bao
ngoài
của
một
parabol.
Clip về Neile Parabola:
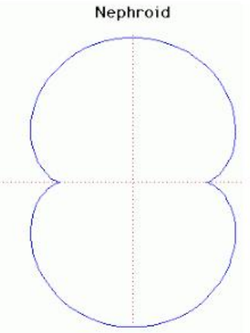
40. Nephroid (Đường cong Nephroid)[sửa]
Phương trình tham số trong hệ tọa độ Descartes:
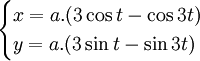
Nephroid (có nghĩa là "hình quả thận ') là tên của đường cong epicycloid có 2 điểm lùi, do Proctor phát hiện vào năm 1878. Nephroid là đường epicycloid được hình thành bởi một đường tròn bán kính a lăn không trượt bên ngoài một đường tròn cố định có bán kính 2a.
Nephroid
có
chiều
dài
là
24a
và
diện
tích
là
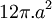 .
.
Năm 1678, Huygens chỉ ra rằng nephroid là catacaustic của một đường tròn khi các nguồn ánh sáng ở vô cực. Ông đã chứng tỏ điều này trong tác phẩm Traité de la lumièrein 1690. Đây cũng là lời giải thích tại sao điều này đã không được phát hiện ra mãi cho đến khi lý thuyết sóng ánh sáng được ứng dụng. Airy đã đưa ra luận chứng lý thuyết về điều này năm 1838.
R.A. Proctor là một nhà toán học người Anh. Ông sinh năm 1837 và qua đời vào năm 1888. Năm 1878, ông xuất bản cuốn " hình học các đường cycloid " tại London. Đường bao trong của nephroid là đường sextic - Cayley hoặc là một nephroid khác vì chúng là những đường cong song song nhau.
Các clips mô tả Nephroid.
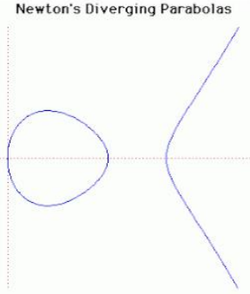
41. Newton’s Diverging Parabolas (Đường parabola phân kỳ Newton)[sửa]
Phương trình đường cong trong hệ tọa độ Descartes:
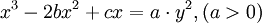
Newton đã phân loại các đường cong bậc 3 trong cuốn "Curves by Sir Isaac Newton in Technicum Lexicon", NXB John Harris xuất bản ở London năm 1710. Trong phân loại các đường cong bậc 3, Newton đưa ra bốn lớp phương trình. Lớp thứ ba của phương trình là một trong những đường cong ở trên mà Newton chia thành năm loại. Trong đó ở trường hợp thứ ba, Newton phát biểu:
Trong
trường
hợp
thứ
ba
phương
trình
là
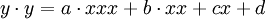 và
định
nghĩa
một
Parabola
có
nhánh
phân
ra
từ
một
nhánh
khác,
và
chạy
ra
vô
hạn
theo
chiều
ngược
lại.
Trường
hợp
phân
chia
thành
năm
loại
này
Newton
đưa
ra
đồ
thị
điển
hình
cho
từng
loại.
Năm
loại
này
phụ
thuộc
vào
nghiệm
của
biểu
thức
bậc
3
ở
vế
phải
của
phương
trình.
và
định
nghĩa
một
Parabola
có
nhánh
phân
ra
từ
một
nhánh
khác,
và
chạy
ra
vô
hạn
theo
chiều
ngược
lại.
Trường
hợp
phân
chia
thành
năm
loại
này
Newton
đưa
ra
đồ
thị
điển
hình
cho
từng
loại.
Năm
loại
này
phụ
thuộc
vào
nghiệm
của
biểu
thức
bậc
3
ở
vế
phải
của
phương
trình.
(i) Tất cả các nghiệm là thực và khác nhau: đồ thị là một Parabola phân kỳ có dạng chuông Bell, với hình Oval tại đỉnh của nó. Đây là trường hợp cho ta đồ thị đường cong như trên.
(ii) Hai nghiệm thực bằng nhau: một Parabola sẽ được hình thành, hoặc là đường cong Nodated có liên quan đến hình Oval, hoặc là đường Punctate, có được từ hình Oval vô cùng nhỏ.
(iii) Ba nghiệm thực bằng nhau: đây là Parabola Neile, thường được gọi là parabola bán-lập phương.
(iv) Chỉ có một nghiệm thực: Nếu hai nghiệm kia là phức, sẽ có một Parabola chính quy dạng hình chuông.
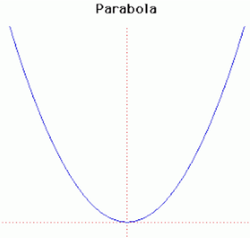
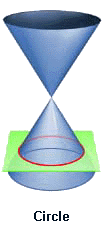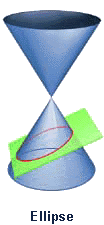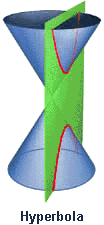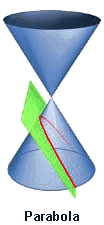
42. Parabola (Đường parabola)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
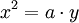 hoặc
hoặc
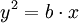
Parabol
được
nghiên
cứu
bởi
Menaechmus,
ông
là
học
trò
của
Plato
và
Eudoxus.
Ông
đã
cố
gắng
tìm
cạnh
của
một
khối
lập
phương
có
thể
tích
gấp
đôi
thể
tích
một
khối
lập
phương
cho
trước.
Từ
đó,
dẫn
đến
việc
đi
tìm
lời
giải
của
phương
trình
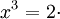 bằng
phương
pháp
hình
học.
bằng
phương
pháp
hình
học.
Trong
thực
tế,
(nhưng
Menaechmus
đã
không
biết
rằng)
bài
toán
này
không
thể
giải
được
bằng
các
phương
pháp
hình
học
sử
dụng
com-pa
và
thước
kẻ.
Menaechmus
đã
giải
quyết
nó
bằng
cách
tìm
các
giao
điểm
của
hai
parabol
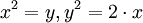
Euclid đã viết về parabol và Apollonius là người đặt tên cho đường cong này. Pappus cũng đã nghiên cứu về tiêu điểm và đường chuẩn của một parabol.
Pascal khảo sát parabol là hình chiếu của một đường tròn và Galileo chứng tỏ rằng đạn đạo là đường cong parabol.
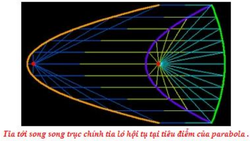
Gregory và Newton đã nghiên cứu các tính chất của parabol khi các tia sáng song song đều hội tụ tại tiêu điểm.
Parabola là quỹ tích những điểm chuyển động M sao cho khoảng cách từ điểm đó đến tiêu điểm F và đường chuẩn (D) bằng nhau: MF = d [ M / (D) ]
Xem chuyển động của các tiếp tuyến của parabola.
Tham khảo[sửa]
1. http://www-history.mcs.st-andrews.ac.uk/Curves/Curves.html
2. http://www-history.mcs.st-andrews.ac.uk/
3. Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers. Department of Mathematics, Computer Science, and Statistics,Bloomsburg University Bloomsburg, Pennsylvania 17815.
4. A Handbook on curves and their properties. Robert C. Yates, printed by Edwards Brothers, Inc - Ann Arbor, Michigan U.S.A.
Bản quyền[sửa]
Biên tập và trích dịch.
Ngày 01/04/2012
Mục lục[sửa]
- Giới thiệu
- Phần 1. Từ As đến Co (1 – 10)
- Phần 2. Từ Co đến Eq (11 – 21)
- Phần 3. Từ Fe đến Ka (22 – 32)
- Phần 4. Từ Ka đến Pa (33 – 42)
- Phần 5. Từ Pe đến Rh (43 – 48)
- Phần 6. Từ Ri đến Sp (49 – 53)
- Phần 7. Từ Sp đến Tr (54 – 58)
- Phần 8. Từ Tr đến Wi (59 – 63)
Bài liên quan
Liên kết đến đây
- Danh mục và lịch sử các đường cong
- Bản mẫu:Danh mục và lịch sử các đường cong
- Danh mục và lịch sử các đường cong/Phần 1. Từ As đến Co (1 – 10)
- Danh mục và lịch sử các đường cong/Phần 2. Từ Co đến Eq (11 – 21)
- Danh mục và lịch sử các đường cong/Phần 3. Từ Fe đến Ka (22 – 32)
- Danh mục và lịch sử các đường cong/Phần 5. Từ Pe đến Rh (43 – 48)
- Danh mục và lịch sử các đường cong/Phần 6. Từ Ri đến Sp (49 – 53)
- Danh mục và lịch sử các đường cong/Phần 7. Từ Sp đến Tr (54 – 58)
- Danh mục và lịch sử các đường cong/Phần 8. Từ Tr đến Wi (59 – 63)