Danh mục và lịch sử các đường cong/Phần 5. Từ Pe đến Rh (43 – 48)
Mục lục
- 1 43. Pearls of de Sluze (Đường viền Sluze)
- 2 44. Pear-Shaped Quartic (Đường bậc 4 hình lê)
- 3 45. Plateau Curves (Đường cong Plateau)
- 4 46. Pursuit Curve (Đường cong đuổi – Bouguer)
- 5 47. Quadratrix of Hippias (Đường bốn đỉnh Hippias)
- 6 48. Rhodonea Curves (Đường cong Rhodonea)
- 7 Tham khảo
- 8 Bản quyền
- 9 Mục lục
43. Pearls of de Sluze (Đường viền Sluze)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
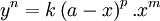
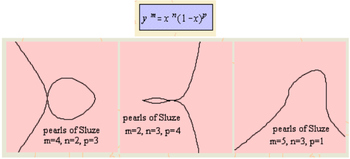
Đường cong với phương trình nêu trên, trong đó n, p, m và n là các số nguyên, đã được de Sluze nghiên cứu khoảng từ 1657 và 1698. Đường viền Sluze là tên đã được Blaise Pascal đặt cho những đường cong này.
Các đường cong cụ thể ở trên có n = 4, k = 2, a = 4, p = 3, m = 2.
René de Sluze được rửa tội ngày 07 tháng 7 năm 1622, khi mới được năm ngày tuổi. Tên của ông xuất hiện theo nhiều cách viết hình thức khác nhau, đây là tính cách phổ biến vào thời đại đó. Có lẽ tên tiếng Pháp phổ biến nhất của tên ông là 'Sluse', nhưng phiên bản Latin 'Slusius' lại là một danh xưng luôn được sử dụng trong văn bản và thư tín khoa học quốc tế của ông.
De Sluze đã nghiên cứu dân luật và giáo luật tại Đại học Louvain từ mùa thu năm 1638 đến mùa hè năm 1642 và nhận bằng tiến sĩ luật trong tháng 10 năm 1643.
Ông bắt đầu sự nghiệp nghiên cứu các đối tượng bao gồm nhiều ngôn ngữ như tiếng Hy Lạp, tiếng Do Thái, tiếng Ả Rập và tiếng Syria, cũng như toán học và thiên văn học tại Đại học Sapienza.
De Sluze đã đọc được nhiều phát hiện toán học mới nhất thông qua việc nghiên cứu các tác phẩm của nhà toán học Ý Bonaventura Cavalieri và Evangelista Torricelli. Ngày 14 tháng 3 năm 1658, De Sluze viết thư cho Christiaan Huygens thông báo về việc tích phân các đường cissoid. Một vài tuần sau khi de Sluze đã xác định thể tích tròn xoay của cissoid, Huygens tìm ra cách cầu phương cho đường cong này. Huygens đã công bố kết quả cho de Sluze ngày 5 tháng 4 năm 1658 và tiếp theo ngày 28 tháng 5 năm 1658, ông đã gửi kết quả chứng minh công thức.
Họ
các
đường
cong
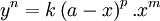 với
các
số
mũ
nguyên
dương,
được
gọi
là
"
đường
viền
Sluze
".
R.
De
Sluze
đã
thảo
luận
những
đường
cong
cũng
như
bài
toán
thể
tích
tròn
xoay
được
tạo
ra
bằng
cách
quay
cissoid
quanh
tiệm
cận
của
nó
trong
tác
phẩm
Miscellanie.
Vài
hình
dạng
đặc
biệt
của
đường
viền
Sluze
như
sau
với
các
số
mũ
nguyên
dương,
được
gọi
là
"
đường
viền
Sluze
".
R.
De
Sluze
đã
thảo
luận
những
đường
cong
cũng
như
bài
toán
thể
tích
tròn
xoay
được
tạo
ra
bằng
cách
quay
cissoid
quanh
tiệm
cận
của
nó
trong
tác
phẩm
Miscellanie.
Vài
hình
dạng
đặc
biệt
của
đường
viền
Sluze
như
sau
44. Pear-Shaped Quartic (Đường bậc 4 hình lê)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
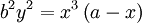
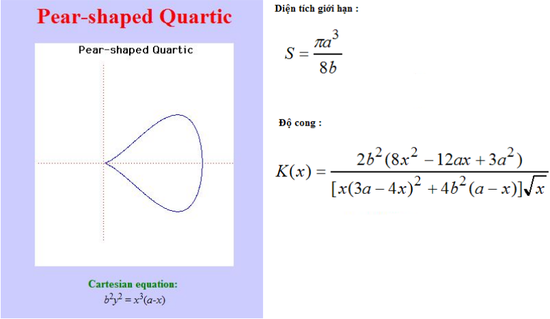
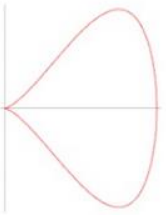
Đường cong này đã được nghiên cứu bởi G. de Longchamps năm 1886. G. de Longchamps cũng nghiên cứu một số đường cong khác mang tên ông.
Gaston Albert Gohierre de Longchamps (1842-1906) là một nhà toán học Pháp, sinh ngày 01 tháng 3 1842, Alençon. Ông học tại École Normale Supérieure đầu năm 1863, và khởi nghiệp là giáo viên vào năm 1866. Ông nghỉ hưu từ Lycée Saint-Louis, là nơi giảng dạy cuối cùng của ông vào năm 1897, và qua đời tại Paris vào ngày 09 tháng bảy 1906.
De Longchamps cũng là thành viên của nhiều tổ chức khoa học, xã hội quốc tế, năm ông 1892 nhận tước Hiệp sĩ và được trao Bắc đẩu bội tinh. Ông là biên tập viên của tạp chí Journal de mathématiques élémentaires và một tạp chí khác có liên quan là Journal de mathématiques spéciales, sau đó De Longchamps quản lý cả hai tạp chí trên được giao từ người sáng lập J. Bourget sau khi ông này mất năm 1887. + Đọc thêm về công trình của G. De Longchamps:
Một
đường
cong
bậc
4
còn
gọi
là
đường
cong
quay
(peg
top)
có
phương
trình
Cartesian
là
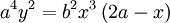 và
phương
trình
tham
số
và
phương
trình
tham
số
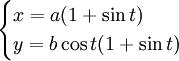
Với
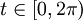 ,
do
nhà
toán
học
G.
de
Longchamps
nghiên
cứu
1886.
,
do
nhà
toán
học
G.
de
Longchamps
nghiên
cứu
1886.
Diện
tích
của
piriform
là
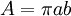
Độ cong (curvature) của piriform được tính bởi
![K(t)={\frac {ab[2+3\sin t+\sin(3t)]}{2\{a^{2}\cos ^{2}t+b^{2}[\cos(2t)-\sin t]^{2}]\}^{{3/2}}}}](https://tusach.thuvienkhoahoc.com/images/math/0/9/d/09d659f5a315e8529bc47e1bf3f3a783.png)
Mã nhúng:
<iframe src="http://www.slideshare.net/slideshow/embed_code/14271268" width="479" height="511" frameborder="0" marginwidth="0" marginheight="0" scrolling="no" style="border:1px solid #CCC; border-width:1px 1px 0; margin-bottom:5px; max-width: 100%;" allowfullscreen></iframe>
45. Plateau Curves (Đường cong Plateau)[sửa]
Phương trình tham số trong hệ tọa độ Descartes:
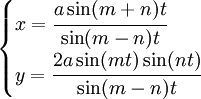
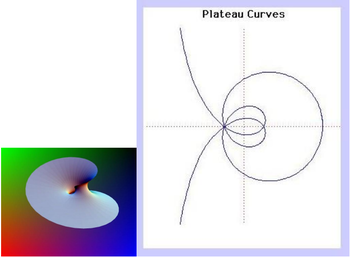
Đường cong này được nghiên cứu bởi nhà vật lí kiêm toán học gia người Bỉ Joseph Plateau.
Nếu m = 2n đường cong Plateau trở thành một đường tròn, có tâm I (1, 0) và bán kính bằng 2. Các đường cong cụ thể ở trên có thông số m = 5, n = 3
Joseph Antoine Ferdinand Plateau ( 1801 - 1883 ) là nhà toán học Bỉ , người có nhiều đóng góp cho cả lĩnh vực vật lý . Cha của Joseph Plateau là một nghệ sĩ tài năng về hội họa. Ông muốn Joseph theo đuổi một sự nghiệp về nghệ thuật và việc học tập của ông đã được tổ chức với mục đích này.
Sau khi tốt nghiệp xuất sắc ở trường tiểu học, Joseph đã được gửi cho Viện Hàn lâm Mỹ thuật. Năm 1822, Joseph Plateau tốt nghiệp trường Athenaeum với văn bằng xuất sắc. Gia sư của J. Plateau khuyên ông nên nghiên cứu văn học và triết học tại Đại học Liège, nhưng Plateau đã quyết định sẽ hoàn thành khóa học và sau đó vẫn đăng ký học các môn mà ông thực sự yêu thích. Joseph Plateau đã thực hiện đúng điều đó, đồng thời nghiên cứu các khóa về toán học và vật lý tại Đại học Liège, ông đã được trao bằng tiến sĩ ngày 03 tháng 6 năm 1829. Trong giới toán học ông được nhớ đến nhiều nhất với bài toán Plateau.Ông cũng viết một số bài báo về lý thuyết số và có một bài viết chung với Quetelet.
Joseph Plateau đã nhận được nhiều danh hiệu cao quý. Ông được bầu là thành viên của Viện Hàn lâm Khoa học Hoàng gia Bỉ (Académie Royale des Sciences, des Lettres et des Beaux Arts) vào ngày 15 Tháng 4 năm 1834 và được bầu là thành viên chính thức vào ngày 15 Tháng 12 năm 1836. Ông đã được trao giải thưởng về toán và vật lý hai lần, lần đầu tiên vào năm 1854 cho công trình nghiên cứu trong giai đoạn 1849-1853, sau đó lần thứ hai vào năm 1869 trong giai đoạn 1864-1868. Ngày 13 Tháng 12 năm 1841, ông được phong tước Knight of Order of Leopold về những đóng góp hữu ích cho khoa học.
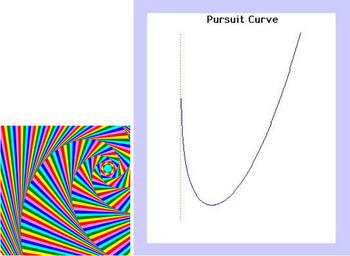
46. Pursuit Curve (Đường cong đuổi – Bouguer)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
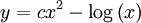
Nếu điểm A di chuyển dọc theo một đường cong cho trước thì điểm P mô tả một đường cong đuổi nếu P luôn hướng về phía A và hai điểm A và P cùng di chuyển với vận tốc đều. Nhà khoa học Pháp Pierre Bouguer đã xem xét hệ chuyển động này trong trường hợp tổng quát năm 1732.
Trường hợp đặc biệt, khi A di động trên một đường thẳng đã được nghiên cứu bởi
Pierre Bouguer (1698 - 1758 ) là một nhà khoa học Pháp, người đầu tiên cố gắng đo tỷ trọng của Trái đất bằng cách sử dụng độ lệch của một dây dọi căn cứ theo sự hấp dẫn của một ngọn núi. Ông đã thực hiện đo đạc ở Peru năm 1740. Một ứng dụng thành công của phương pháp này là của nhà thiên văn học Maskelyne, đã quy định tỷ trọng trái đất từ 4,5 đến 5.
Cha của Pierre Bouguer, Jean Bouguer, là Giáo sư Hoàng gia thủy văn. Jean Bouguer dạy Pierre cậu con trai của mình cả toán học và thuỷ văn, và Pierre hóa ra lại là một học sinh xuất sắc trong cả hai lĩnh vực. Pierre đã có một sự hiểu biết rất sâu sắc về toán học, khoa học và là một thần đồng thực sự ở tuổi mười lăm.
Sau đó, một điều đáng chú ý đã xảy ra. Jean Boutroux chết khi Pierre mới mười lăm tuổi và do đó, vị trí Giáo sư Hoàng gia thủy văn bị bỏ trống. Pierre được bổ nhiệm vào chức vụ giáo sư của cha mình và ông trở thành nhân vật đáng chú ý, vừa thông minh vừa học cao hiểu rộng. Năm 1727, Pierre Bouguer đã giành được giải Grand Prix của Viện khoa học Hoàng gia (Académie Royale des Sciences) về công trình nghiên cứu cột buồm.Hai năm sau ông lại giành giải thưởng lớn, với một tiểu luận về quan sát độ cao của các ngôi sao trên biển. Sau đó, 1731, ông đã giành giải ba Grand Prix của Académie Royale des Sciences cho công trình nghiên cứu về độ từ thiên (magnetic declination) trên biển.
Académie Royale des Sciences tiếp tục vinh danh Piere Bouguer khi ông được bầu là phó viện sĩ toán học năm 1731 và sau đó, vào năm 1735, ông được bầu làm viện sĩ chính thức. Năm 1732, Bouguer nghiên cứu các đường cong đuổi và viết một bài báo về đề tài này. Tháng 4 năm 1735 Bouguer bắt đầu cuộc thám hiểm, do Académie Royale des Sciences tổ chức, đến Peru để đo chiều dài của kinh tuyến tại đường xích đạo
Bouguer đã viết một số bài về kỹ thuật thao diễn hải quân và khoa học hàng hải, về kỹ thuật thiết kế tàu, phát minh một công thức để tính toán bán kính metacentric (một biện pháp ổn định tàu).
Tuy nhiên, đóng góp xuất sắc nhất cho lĩnh vực khoa học mà ông coi là một sở thích trong nhiều năm là trắc quang và chính điều này đã vinh danh ông là "cha đẻ của ngành trắc quang học (photometry)".
Bắt đầu từ năm 1721, ông đã thực hiện một số các phép đo đầu tiên của quang học thiên văn. Ông đã so sánh độ sáng của mặt trăng với độ sáng của một ngọn lửa nến tiêu chuẩn vào ngày 23 tháng 11, 1725.
Ông đã xuất bản cuốn " Essai d'optique sur la gradation de la lumière " năm 1729. Công trình này có chứa khám phá vĩ đại thứ hai của Bouguer liên quan đến ánh sáng, cụ thể là định luật Bouguer, thể hiện mối quan hệ giữa sự hấp thụ năng lượng bức xạ và môi trường hấp thụ.
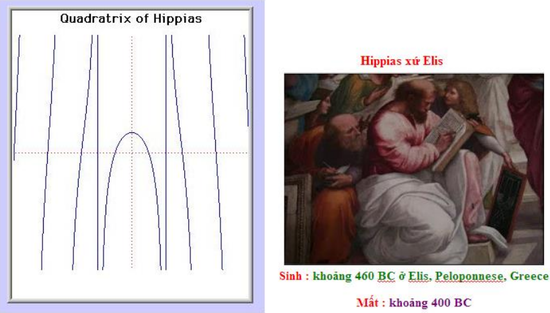
47. Quadratrix of Hippias (Đường bốn đỉnh Hippias)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
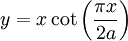
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
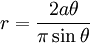
Hippias ( ~ 460 BC - ~400 BC) là nhà toán học nghiệp dư xứ Elis , Hy Lạp . Đường cong Quadratrix được Hippias phát hiện năm 430 trước Công nguyên. Có lẽ ông đã sử dụng cho việc giải bài toán chia một góc làm 3 phần và bình phương vòng tròn. Đường cong này được sử dụng để phân chia một góc bất kỳ thành một số góc nhỏ bằng nhau.
Sau đó, Dinostratus tiếp tục nghiên cứu bài toán này vào 350 trước Công nguyên. Heath kể cho chúng ta một điều gì đó của nhân vật này khi ông đã viết trong " Chronology: 500BC to 1AD " như sau:
" Hippias tuyên bố... đã có lần đến các lễ hội Olympic với tất cả mọi thứ mà ông mặc trên mình, chiếc nhẫn và sandal bóng loáng, dầu thơm hương phấn, quần áo diêm dúa, và dây nịt xứ Ba Tư loại đắt tiền; ông cũng đem theo những bài thơ, sử thi, bi kịch, và tất cả các bản văn xuôi... "
Về thành tích học tập của Hippias, Heath viết:
"Ông là một bậc thầy của khoa học tính toán, hình học, thiên văn học. Hippias cũng đã có một hệ thống trí nhớ tuyệt vời, để nếu ông đã từng nghe đọc một chuỗi năm mươi tên gọi thì có thể nhớ được tất cả. "
Heath cũng đã viết rằng:
"Dường như là khoảng 420 trước Công nguyên, Hippias xứ Elis đã phát minh ra đường cong được gọi là quadratrix khi giải quyết bài toán chia 3 một góc bất kỳ. "
Pappus khi viết tác phẩm lớn của ông về hình học Synagoge năm 340, là một bộ sưu tập các tác phẩm toán học trong tám cuốn sách, trong đó quyển IV cũng ghi lại sự mô tả về quadratrix của Hippias xứ Elis.
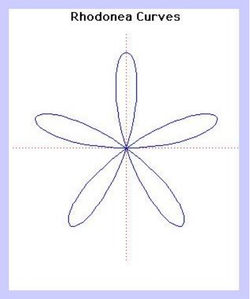
48. Rhodonea Curves (Đường cong Rhodonea)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
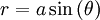
Những đường cong này được đặt tên theo nhà toán học người Ý Guido Grandi khoảng giữa 1723 và 1728, vì chúng trông giống như hoa hồng.
Khi k là một số nguyên thì sẽ có k hay 2k cánh hoa tùy thuộc vào k là lẻ hoặc chẵn.
Nếu k là vô tỷ thì số lượng cánh hoa là vô hạn.
Quadrifolium
(đường
cong
4
lá)
là
những
đường
cong
rhodonea
với
k
=
2.
Có
phương
trình
cực
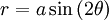 và
dạng
Descartes
và
dạng
Descartes
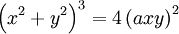
Luigi Guido Grandi ( 1671 - 1742 ) . Sinh năm 1671, linh mục, nhà triết học, nhà toán học và kỹ sư Luigi Guido Grandi được sinh ra ở Cremona, nước Ý. Trong toán học, ông được biết đến với những nghiên cứu về các đường cong hoa hồng và chuỗi Grandi. Ông đã có một số đóng góp cho các công trình của Galileo Galilei và có công lớn trong việc giới thiệu phép tính calculus đến Ý.
Luigi Guido Grandi là một thành viên của Camaldolites. Ông trở thành giáo sư triết học vào năm 1700 và là giáo sư toán học vào năm 1714, cả hai vị trí này đều tại Đại học Pisa.
Guido Grandi đầu tiên học tại trường đại học Dòng Tên ở Cremona. Ông trở thành một thành viên của Dòng tu Camaldolese vào năm 1687. Sau đó, năm 1693, ông chuyển đến tu viện của Dòng Camaldolese ở Rome.
Năm sau, Grandi đã trở thành một giáo viên triết học và thần học tại tu viện Camaldolese ở Florence., Lúc trước ông ít quan tâm trong toán học nhưng đến thời gian này ông đã bắt đầu thay đổi hướng suy nghĩ. Tuy nhiên, ông tiếp tục giảng dạy triết học, được bổ nhiệm làm giáo sư tại Rome vào năm 1700, sau đó chuyển đến Pisa một lần nữa với vai trò giáo sư triết học. Sự kiện đến với toán học đầu tiên của Grandi là năm 1707, khi ông trở thành nhà toán học của đại công tước xứ Tuscany, Cosimo III de 'Medici. Năm 1709, ông viếng thăm Anh quốc và thực sự gây ấn tượng cho các nhà khoa học Anh khi ông được bầu là Uỷ viên của Hội Hoàng gia. Năm 1714, Grandi được bổ nhiệm làm Giáo sư Toán học tại Đại học Pisa.
Grandi là tác giả của một số công trình về hình học, trong đó ông nghiên cứu sự tương tự của đường tròn và hyperbola đều. Ông cũng khảo sát các đường cong có độ cong đôi trên mặt cầu và cầu phương từng phần của một bề mặt hình cầu.
Vào năm 1701, Grandi thảo luận về đường tà hình nón - đường cong cắt đường sinh của một hình nón tròn xoay theo một góc không đổi. Ông cũng nghiên cứu các đường cong Phù thủy Agnesi năm 1703. Trong thực tế, công trình quan trọng nhất của ông vào năm 1703 là giới thiệu phép tính của Leibniz (Calculus) vào Italy.
Năm 1728 Grandi xuất bản tác phẩm " Flores Geometrici ", một công trình mà trong đó ông đưa ra định nghĩa đường cong clelie. Ông đặt tên cho các đường cong theo tên nữ bá tước Clelia Borromeo và dành tặng cuốn sách của mình cho cô. Nếu kinh độ và dư vĩ độ của một điểm P trên một hình cầu được ký hiệu là θ và φ và nếu P di chuyển sao cho θ = φ m, với m là một hằng số, thì quỹ tích của P là một đường cong clelie. Grandi thường áp dụng thuật ngữ "clelies" cho các đường cong được xác định bởi các phương trình lượng giác liên quan đến hàm sin
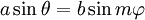
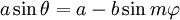
Grandi cũng nghiên cứu hệ thống thuỷ lực và đã tham gia vào một số dự án, chẳng hạn như những hệ thống thủy lợi Chiana Valley và Pontine Marshes. Ông cũng công bố một số công trình về cơ học và thiên văn học. Những đề tài thực hành của ông về cơ học bao gồm các thí nghiệm về động cơ hơi nước.
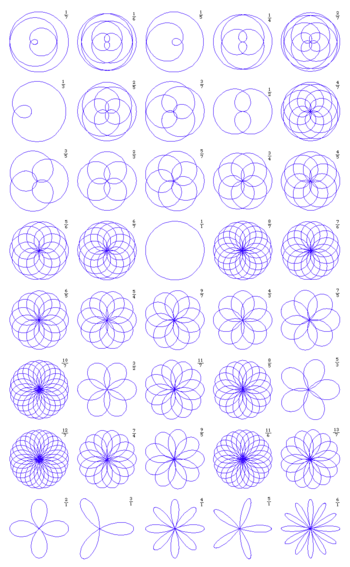
Dưới đây là bộ sưu tập các đường cong thuộc họ rhodonea.
Tham khảo[sửa]
1. http://www-history.mcs.st-andrews.ac.uk/Curves/Curves.html
2. http://www-history.mcs.st-andrews.ac.uk/
3. Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers. Department of Mathematics, Computer Science, and Statistics,Bloomsburg University Bloomsburg, Pennsylvania 17815.
4. A Handbook on curves and their properties. Robert C. Yates, printed by Edwards Brothers, Inc - Ann Arbor, Michigan U.S.A.
Bản quyền[sửa]
Biên tập và trích dịch.
Ngày 01/04/2012
Mục lục[sửa]
- Giới thiệu
- Phần 1. Từ As đến Co (1 – 10)
- Phần 2. Từ Co đến Eq (11 – 21)
- Phần 3. Từ Fe đến Ka (22 – 32)
- Phần 4. Từ Ka đến Pa (33 – 42)
- Phần 5. Từ Pe đến Rh (43 – 48)
- Phần 6. Từ Ri đến Sp (49 – 53)
- Phần 7. Từ Sp đến Tr (54 – 58)
- Phần 8. Từ Tr đến Wi (59 – 63)
Bài liên quan
Liên kết đến đây
- Danh mục và lịch sử các đường cong
- Bản mẫu:Danh mục và lịch sử các đường cong
- Danh mục và lịch sử các đường cong/Phần 1. Từ As đến Co (1 – 10)
- Danh mục và lịch sử các đường cong/Phần 2. Từ Co đến Eq (11 – 21)
- Danh mục và lịch sử các đường cong/Phần 3. Từ Fe đến Ka (22 – 32)
- Danh mục và lịch sử các đường cong/Phần 4. Từ Ka đến Pa (33 – 42)
- Danh mục và lịch sử các đường cong/Phần 6. Từ Ri đến Sp (49 – 53)
- Danh mục và lịch sử các đường cong/Phần 7. Từ Sp đến Tr (54 – 58)
- Danh mục và lịch sử các đường cong/Phần 8. Từ Tr đến Wi (59 – 63)